Type I and II Errors

COMMON MISTEAKS MISTAKES IN USING STATISTICS: Spotting and Avoiding Them

Introduction Types of Mistakes Suggestions Resources Table of Contents About

Type I and II Errors and Significance Levels

Type I Error

Rejecting the null hypothesis when it is in fact true is called a Type I error.

Many people decide, before doing a hypothesis test, on a maximum p-value for which they will reject the null hypothesis. This value is often denoted α (alpha) and is also called the significance level.

When a hypothesis test results in a p-value that is less than the significance level, the result of the hypothesis test is called statistically significant.

Common mistake: Confusing statistical significance and practical significance.

Example: A large clinical trial is carried out to compare a new medical treatment with a standard one. The statistical analysis shows a statistically significant difference in lifespan when using the new treatment compared to the old one. But the increase in lifespan is at most three days, with average increase less than 24 hours, and with poor quality of life during the period of extended life. Most people would not consider the improvement practically significant.

Caution: The larger the sample size, the more likely a hypothesis test will detect a small difference. Thus it is especially important to consider practical significance when sample size is large.

Connection between Type I error and significance level:

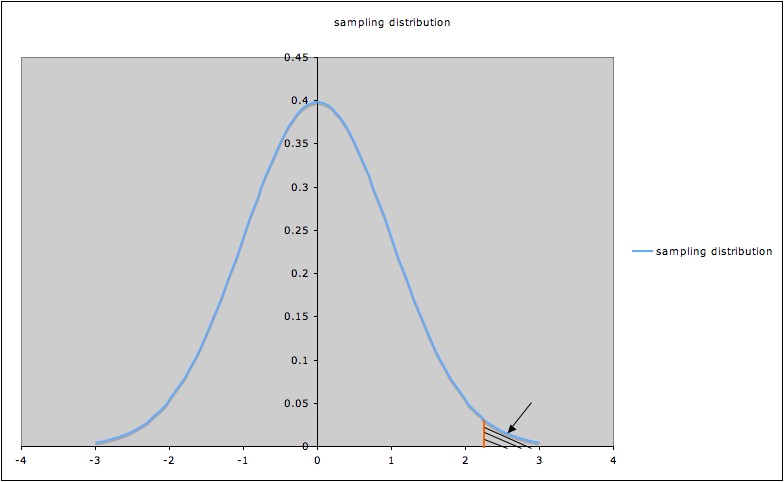
A significance level α corresponds to a certain value of the test statistic, say t_α, represented by the orange line in the picture of a sampling distribution below (the picture illustrates a hypothesis test with alternate hypothesis "µ > 0")

Since the shaded area indicated by the arrow is the p-value corresponding to t_α, that p-value (shaded area) is α.
To have p-value less than α , a t-value for this test must be to the right of t_α.
So the probability of rejecting the null hypothesis when it is true is the probability that t > t_α, which we saw above is α.
In other words, the probability of Type I error is α.¹

Rephrasing using the definition of Type I error:

The significance level α is the probability of making the wrong decision when the null hypothesis is true.

Pros and Cons of Setting a Significance Level:

Setting a significance level (before doing inference) has the advantage that the analyst is not tempted to chose a cut-off on the basis of what he or she hopes is true.

It has the disadvantage that it neglects that some p-values might best be considered borderline. This is one reason² why it is important to report p-values when reporting results of hypothesis tests. It is also good practice to include confidence intervals corresponding to the hypothesis test. (For example, if a hypothesis test for the difference of two means is performed, also give a confidence interval for the difference of those means. If the significance level for the hypothesis test is .05, then use confidence level 95% for the confidence interval.)

Type II Error

Not rejecting the null hypothesis when in fact the alternate hypothesis is true is called a Type II error. (The second example below provides a situation where the concept of Type II error is important.)

Note: "The alternate hypothesis" in the definition of Type II error may refer to the alternate hypothesis in a hypothesis test, or it may refer to a "specific" alternate hypothesis.

Example: In a t-test for a sample mean µ, with null hypothesis ""µ = 0" and alternate hypothesis "µ > 0", we may talk about the Type II error relative to the general alternate hypothesis "µ > 0", or may talk about the Type II error relative to the specific alternate hypothesis "µ > 1". Note that the specific alternate hypothesis is a special case of the general alternate hypothesis.

In practice, people often work with Type II error relative to a specific alternate hypothesis. In this situation, the probability of Type II error relative to the specific alternate hypothesis is often called β. In other words, β is the probability of making the wrong decision when the specific alternate hypothesis is true.

(See the discussion of Power for related detail.)

Considering both types of error together:

The following table summarizes Type I and Type II errors:

		Truth (for population studied)
		Null Hypothesis True	Null Hypothesis False
Decision (based on sample)	Reject Null Hypothesis	Type I Error	Correct Decision
Decision (based on sample)	Fail to reject Null Hypothesis	Correct Decision	Type II Error

An analogy³ that some people find helpful (but others don't) in understanding the two types of error is to consider a defendant in a trial. The null hypothesis is "defendant is not guilty;" the alternate is "defendant is guilty."⁴A Type I error would correspond to convicting an innocent person; a Type II error would correspond to setting a guilty person free. The analogous table would be:

		Truth
		Not Guilty	Guilty
Verdict	Guilty	Type I Error -- Innocent person goes to jail (and maybe guilty person goes free)	Correct Decision
Verdict	Not Guilty	Correct Decision	Type II Error -- Guilty person goes free

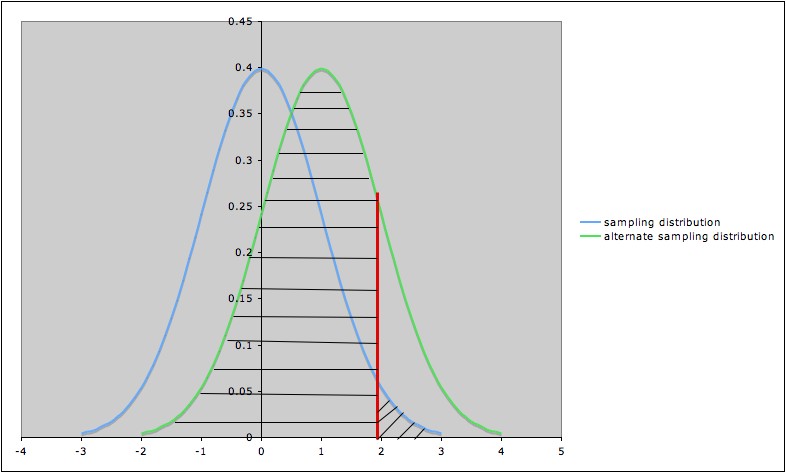
The following diagram illustrates the Type I error and the Type II error against the specific alternate hypothesis "µ =1" in a hypothesis test for a population mean µ, with null hypothesis ""µ = 0," alternate hypothesis "µ > 0", and significance level α= 0.05.

The blue (leftmost) curve is the sampling distribution assuming the null hypothesis ""µ = 0."

The green (rightmost) curve is the sampling distribution assuming the specific alternate hypothesis "µ =1".

The vertical red line shows the cut-off for rejection of the null hypothesis: the null hypothesis is rejected for values of the test statistic to the right of the red line (and not rejected for values to the left of the red line)>

The area of the diagonally hatched region to the right of the red line and under the blue curve is the probability of type I error (α)

The area of the horizontally hatched region to the left of the red line and under the green curve is the probability of Type II error (β)

Sampling disttibution for null and specifi alternate hypothesis, showing Types I and II errors

Deciding what significance level to use:

This should be done before analyzing the data -- preferably before gathering the data.⁵
The choice of significance level should be based on the consequences of Type I and Type II errors.

If the consequences of a type I error are serious or expensive, then a very small significance level is appropriate.

Example 1: Two drugs are being compared for effectiveness in treating the same condition. Drug 1 is very affordable, but Drug 2 is extremely expensive. The null hypothesis is "both drugs are equally effective," and the alternate is "Drug 2 is more effective than Drug 1." In this situation, a Type I error would be deciding that Drug 2 is more effective, when in fact it is no better than Drug 1, but would cost the patient much more money. That would be undesirable from the patient's perspective, so a small significance level is warranted.

If the consequences of a Type I error are not very serious (and especially if a Type II error has serious consequences), then a larger significance level is appropriate.

Example 2: Two drugs are known to be equally effective for a certain condition. They are also each equally affordable. However, there is some suspicion that Drug 2 causes a serious side-effect in some patients, whereas Drug 1 has been used for decades with no reports of the side effect. The null hypothesis is "the incidence of the side effect in both drugs is the same", and the alternate is "the incidence of the side effect in Drug 2 is greater than that in Drug 1." Falsely rejecting the null hypothesis when it is in fact true (Type I error) would have no great consequences for the consumer, but a Type II error (i.e., failing to reject the null hypothesis when in fact the alternate is true, which would result in deciding that Drug 2 is no more harmful than Drug 1 when it is in fact more harmful) could have serious consequences from a public health standpoint. So setting a large significance level is appropriate.

See Sample size calculations to plan an experiment, GraphPad.com, for more examples.

Common mistake: Neglecting to think adequately about possible consequences of Type I and Type II errors (and deciding acceptable levels of Type I and II errors based on these consequences) before conducting a study and analyzing data.

Sometimes there may be serious consequences of each alternative, so some compromises or weighing priorities may be necessary. The trial analogy illustrates this well: Which is better or worse, imprisoning an innocent person or letting a guilty person go free?⁶ This is a value judgment; value judgments are often involved in deciding on significance levels. Trying to avoid the issue by always choosing the same significance level is itself a value judgment.

Sometimes different stakeholders have different interests that compete (e.g., in the second example above, the developers of Drug 2 might prefer to have a smaller significance level.)

See http://core.ecu.edu/psyc/wuenschk/StatHelp/Type-I-II-Errors.htm for more discussion of the considerations involved in deciding what are reasonable levels for Type I and Type II errors.

See the discussion of Power for more on deciding on a significance level.

Similar considerations hold for setting confidence levels for confidence intervals.

Common mistake: Claiming that an alternate hypothesis has been "proved" because it has been rejected in a hypothesis test.

This is an instance of the common mistake of expecting too much certainty.
There is always a possibility of a Type I error; the sample in the study might have been one of the small percentage of samples giving an unusually extreme test statistic.

This is why replicating experiments (i.e., repeating the experiment with another sample) is important. The more experiments that give the same result, the stronger the evidence.

There is also the possibility that the sample is biased or the method of analysis was inappropriate; either of these could lead to a misleading result.

1. α is also called the bound on Type I error. Choosing a value α is sometimes called setting a bound on Type I error.

2. Another good reason for reporting p-values is that different people may have different standards of evidence; see the section "Deciding what significance level to use" on this page.

3. This could be more than just an analogy: Consider a situation where the verdict hinges on statistical evidence (e.g., a DNA test), and where rejecting the null hypothesis would result in a verdict of guilty, and not rejecting the null hypothesis would result in a verdict of not guilty.

4. This is consistent with the system of justice in the USA, in which a defendant is assumed innocent until proven guilty beyond a reasonable doubt; proving the defendant guilty beyond a reasonable doubt is analogous to providing evidence that would be very unusual if the null hypothesis is true.

5. There are (at least) two reasons why this is important. First, the significance level desired is one criterion in deciding on an appropriate sample size. (See Power for more information.) Second, if more than one hypothesis test is planned, additional considerations need to be taken into account. (See Multiple Inference for more information.)

6. The answer to this may well depend on the seriousness of the punishment and the seriousness of the crime. For example, if the punishment is death, a Type I error is extremely serious. Also, if a Type I error results in a criminal going free as well as an innocent person being punished, then it is more serious than a Type II error.

Last updated May 12, 2011