
| SMMG Home Current Schedule Video Past Talks Fun Links Contact Information Driving Directions and Parking Math Department Home Problem Solving Challenge |
September 2007
To learn more about Dr. Stone's soccer team, go to the Austin Villa webpage. Here are some pictures of the robot soccer team in action: The talk was a complete success, with a close to record attendance! We were all fascinated with this interesting topic. As promised, here are the power point presentations, in three parts: the first half of the lecture was about machine learning and robot soccer, and the second part focused more on autonomous traffic in intersections, and the DARPA urban challenge. For some pictures of the lecture, click here. The video for this lecture is up! Just click here! October 2007
Here is a handout summarizing some facts about infinity, cardinality and one-to-one correspondences. In the second half of the lecture, we played a game called Dodge Ball, created by Professor Starbird himself with his co-author Edward Burger. Here are some links for the rules of the game , and a copy of the game board. The ideas presented when we were talking about Dodge Ball can be extended to other sets, namely sets of real numbers. The puzzle for this lecture should give a better idea of what happens with some special sets of numbers. For some pictures of the lecture, click here. November 2007
We got a great presentation about how inequalities and approximate answers can play an important role in mathematics. You can now download the presentation slides. For demos and a faster version of the slides you can go to Professor Freed's webpage. There was an activity where we tried to find the area of an irregular shape, and then we used a grid to approximate the area. We made this better by using a finer grid. Click here to see some pictures taken during the lecture. Unfortunately, due to some technical difficulties there will be no video for this lecture. We apologize for the inconvenience. December 2007
Ever since The Silence of the Lambs, the public has been fascinated by psychological profiling and the use of behavioral science to help solve crime. Research on the accuracy and usefulness of these techniques, however, has not always been positive. But while the "art" behind criminal profiling may be problematic, the science is not. That science is based on empirical research in the fields of criminology and psychology and the correct application of probability. We will discuss behavioral profiling (as psychological
profiling is now known), linkage analysis (methods of determining which
crimes were done by the same serial offender), and geographic profiling
(a methodology that uses crime locations to determine where the
offender most likely lives). We will also touch on the role played by
misunderstandings of probability in criminal investigative failures.
Finally, we will examine how the CBS television show, Numb3rs, relates to
the real world of police investigation. Here are a couple of maps used for criminal geographic profiling. 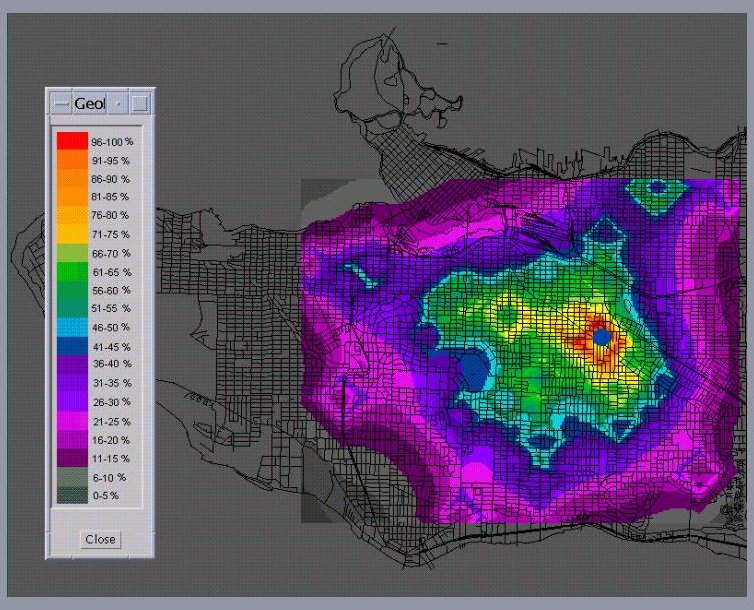 
The talk went great and everyone was captivated by how the use of mathematics led to the apprehension of some pretty bad people. We also learned how misunderstanding mathematics can lead to the imprisonment of innocent people and the failure to convict the right people for their crimes. Here are some pictures of the lecture.
Cody is a 5th year graduate student who has been involved with math camps and math teams since he was an undergraduate. In this workshop, the people who attended got to learn how they could use recursion to count the number of ways to make change for a given amount of money using U.S. coins, and how the Fibonacci sequence (a recursively defined sequence) comes up naturally in certain counting problems. For a PDF file of the lecture, click here. One of the activities required a handout to figure out how many ways you could fill up a grid with a certain shape of tiles. For pictures of the lecture, click here. |





