



Next: Storage Modes
Up: NSPCG User's Guide
Previous: Brief Background on Accelerators
Parameter Arrays IPARM and RPARM
The user must supply default values for the parameters in IPARM
and RPARM by inserting the line
CALL DFAULT (IPARM,RPARM)
in the program before the call to NSPCG. The user may then assign
nondefault values to selected quantities in IPARM and RPARM by
inserting the appropriate assignment statements before the call to
the iterative routine.
Important variables in this package which may change adaptively
are EMAX and EMIN (eigenvalue estimates of Q-1A), OMEGA
(overrelaxation
parameter for the SOR and SSOR methods), ALPHAB and BETAB (SSOR
parameters), and SPECR (estimate of the spectral radius of the SOR
iteration matrix).
The integer vector IPARM and the real vector RPARM allow the user
to control certain parameters which affect the performance of the
iterative algorithms. Furthermore, these vectors allow the updated
parameters from the automatic adaptive procedures to be communicated
back to the user. The IPARM and RPARM parameters are described
below.
Description of IPARM parameters
- IPARM(1)
- (NTEST):
The stopping test number, in the range 1 to 10, indicates
which stopping test should be used to terminate the
iteration. (See Section 10 for a description
of the available stopping tests.) The SOR accelerator
uses a specialized stopping test, so this parameter is
ignored when SOR is called unless
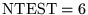 ,
in which
case the exact stopping test is used. [Default: 2]
,
in which
case the exact stopping test is used. [Default: 2]
- IPARM(2)
- (ITMAX):
On input, ITMAX is the maximum number of iterations
allowed. On output, ITMAX is the number of iterations
performed. [Default: 100]
- IPARM(3)
- (LEVEL):
LEVEL is the output level control switch. Each higher
value provides additional information. [Default: 0]
| < 0 |
no output |
| = 0 |
fatal error messages only (default) |
| = 1 |
warning messages and minimum output |
| = 2 |
reasonable summary |
| = 3 |
parameter values and informative comments |
| = 4 |
approximate solution after every iteration |
- IPARM(4)
- (NOUT):
NOUT is the Fortran unit number for output. [Default: 6]
- IPARM(5)
- (IDGTS):
IDGTS is the error analysis switch. An analysis of the
final computed solution is made to determine the
accuracy. [Default: 0]
| < 0 |
skip error analysis |
| = 0 |
compute DIGIT1 and DIGIT2 and store in RPARM
(default) |
| = 1 |
print DIGIT1 and DIGIT2 |
| = 2 |
print final approximate solution vector |
| = 3 |
print final approximate residual vector |
| = 4 |
print both solution and residual vectors |
If LEVEL is less than 1, no printing is done. See
explanation of DIGIT1 [= RPARM(7)] and DIGIT2 [= RPARM(8)]
for more details.
- IPARM(6)
- (MAXADP):
This parameter is the adaptive procedure switch for EMAX.
[Default: 1]
| = 0 |
no adapting on EMAX |
| = 1 |
adapting on EMAX (default) |
- IPARM(7)
- (MINADP):
This parameter is the adaptive procedure switch for EMIN.
[Default: 1]
| = 0 |
no adapting on EMIN |
| = 1 |
adapting on EMIN (default) |
- IPARM(8)
- (IOMGAD):
This parameter is the adaptive procedure switch for OMEGA.
[Default: 1]
| = 0 |
no adapting on OMEGA |
| = 1 |
adapting on OMEGA (default) |
- IPARM(9)
- (NS1):
NS1 is the number of old vectors to be saved for the
truncated acceleration methods. [Default: 5]
- IPARM(10)
- (NS2):
NS2 is the frequency of restarting for the restarted
acceleration methods. By default, NS2 is set to a large
value so that restarting is not done. [Default: 100000]
- IPARM(11)
- (NS3):
Used only in ORTHOMIN, NS3 denotes the size of the largest
Hessenberg matrix to be used to estimate the eigenvalues;
it should be set to some value such as 40. [Default: 0]
- IPARM(12)
- (NSTORE):
NSTORE indicates the storage mode used. See
Section 8 for a description of the storage
modes. [Default: 2]
| = 1 |
Primary format |
| = 2 |
Symmetric diagonal format (default) |
| = 3 |
Nonsymmetric diagonal format |
| = 4 |
Symmetric coordinate format |
| = 5 |
Nonsymmetric coordinate format |
- IPARM(13)
- (ISCALE):
ISCALE is a switch indicating whether or not the matrix
should be scaled before iterating and unscaled after
iterating. [Default: 0]
| = 0 |
no scaling (default) |
| = 1 |
scaling |
If scaling is selected, the matrix is scaled to have a unit
diagonal, and u and b are scaled accordingly. If
NTEST = 6, 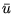 is also scaled.
If Au=b is the system to be scaled, and D is the diagonal
of A, the scaled system is
is also scaled.
If Au=b is the system to be scaled, and D is the diagonal
of A, the scaled system is
The diagonal elements of the matrix must be positive if
scaling is requested. Scaling of the system causes an
extra N elements of WKSP to be used, so scaling is not
recommended if storage is a consideration.
- IPARM(14)
- (IPERM):
IPERM is a switch indicating whether or not the matrix
should be permuted before iterating and unpermuted after
iterating. [Default: 0]
| = 0 |
no permuting (default) |
| = 1 |
permuting |
If a permutation of the matrix is desired, IPERM must be set
to 1, and the vector P of the argument list of NSPCG must
contain a coloring vector. See Sections 11 and
12 for more details on
coloring vectors. If IPERM = 0, the vector P is ignored and
can be dimensioned to be of length one. If IPERM = 1, a
permutation vector is generated from P and replaces it, while
IP contains the inverse permutation vector on output.
If Au=b is the system to be permuted and P is the
permutation vector, the permuted system is
(PAPT) (Pu) = Pb
If NTEST = 6, 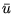 is permuted in addition to
u and b.
is permuted in addition to
u and b.
- IPARM(15)
- (IFACT):
IFACT indicates whether a factorization associated with a
particular preconditioner should be computed for the
current NSPCG call or whether a factorization from a
previous NSPCG call should be used. For some preconditioners,
the factorization time can be a significant percentage of
the iteration time. If one is making a series of calls to
NSPCG (as in a time-dependent or nonlinear application) and
the coefficient matrix is not changing much, it may be
reasonable to amortize the cost of factorization over several
NSPCG calls by using a factor from a previous call for the
current call. The user must call the same preconditioner
for all calls, and the structure of A as indicated by JCOEF
cannot be changing. [Default: 1]
| 1 |
matrix A is to be factored for the current call
(default) |
| 0 |
matrix A is not to be factored for the current
call (previous factorization used) |
- IPARM(16)
- (LVFILL):
LVFILL is the level of point or block fill-in to be allowed
during the factorization. It affects the preconditioners
| ICi |
(i = 1,2,3) |
| MICi |
(i = 1,2,3) |
| BICi |
(i = 2,3) |
| BICXi |
(i = 2,3) |
| MBICi |
(i = 2,3) |
| MBICXi |
(i = 2,3) |
If LVFILL = 0, no fill-in
is allowed beyond the original matrix nonzero pattern. If
LVFILL = 1, fill-in is allowed caused by the original
nonzero pattern, but no further fill-in caused by these just
filled-in elements is allowed. If LVFILL = 2, fill-in is
allowed if it is due to the original pattern or LVFILL = 1 filled-in elements.
As an example of point fill-in, suppose a symmetric
matrix has diagonals at distances of 0, 1, and s.
Then the diagonals of the factorization are:
In general, if at LVFILL = k, the positive diagonal numbers
are
and the negative diagonal numbers are
then the diagonal numbers at LVFILL = k+1 are
In the example above for LVFILL =0, then p1=1,
p2=s, q1=-1, and q2=-s. Hence for LVFILL =1,
the diagonal numbers are
0,1,-1,(s-1),-(s-1),s,-s.
For block factorization methods, LVFILL is the level of
block fill-in. For example, if a 7-point finite difference
stencil is used to discretize a partial differential equation
on a 3-dimensional box domain, the resulting matrix can be
regarded as a block pentadiagonal matrix with 1-D blocks
corresponding to the mesh lines. The block band is sparse
and will tend to fill in during a block factorization. If
LVFILL is positive, line blocks which are zero in the original
matrix will be allowed to fill in with a bandwidth equal
the bandwidth of the diagonal pivot blocks, which in turn
are determined by LTRUNC.
In general, an increase in LVFILL results in a more accurate
factorization (and fewer iterations) but at the expense of
increased storage requirements and possibly more total time.
[Default: 0]
- IPARM(17)
- (LTRUNC):
LTRUNC determines the truncation bandwidth to be used when
approximating the inverses of matrices with dense banded
matrices. It affects the preconditioners LJACXi, BICi,
BICXi, MBICi, MBICXi for i=2,3. If the band matrix
whose inverse is being approximated has a half-bandwidth of
s,
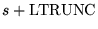 will be the half-bandwidth
of the approximating inverse. Thus, LTRUNC is the increase
in bandwidth to be used for the inverse approximation over
the bandwidth of the original matrix. In general, an
increase in LTRUNC means a more accurate factorization at
the expense of increased storage. [Default: 0]
will be the half-bandwidth
of the approximating inverse. Thus, LTRUNC is the increase
in bandwidth to be used for the inverse approximation over
the bandwidth of the original matrix. In general, an
increase in LTRUNC means a more accurate factorization at
the expense of increased storage. [Default: 0]
- IPARM(18)
- (IPROPA):
IPROPA is a flag to indicate whether or not matrix A has
Property A. If a matrix has Property A, it is two-cyclic
and can be permuted to a red-black matrix. Also, a
considerable savings in storage is possible if a factorization
preconditioner is called. IPROPA affects the following
preconditioners:
| ICi |
(i=1,2,3,6) |
| MICi |
(i=1,2,3,6) |
| BICi |
(i=2,3,7) |
| BICXi |
(i=2,3,7) |
| MBICi |
(i=2,3,7) |
| MBICXi |
(i=2,3,7) |
For the first two preconditioners, IPROPA refers to point
Property A. For the last four preconditioners, IPROPA
refers to block Property A (i.e., whether the matrix
considered as a block matrix has Property A). IPROPA
can assume the following values on input:
| = 0 |
if matrix A does not have Property A |
| = 1 |
if matrix A has Property A |
| = 2 |
if it is not known whether or not matrix A has |
| |
Property A; compute if needed (default) |
If IPROPA = 2 and LVFILL = 0 on input, and one of the
six methods above is used, it is determined whether or
not the matrix has property A, and IPROPA is reset to
0 or 1 accordingly.
Determining if matrix A has Property A requires 2N
workspace from IWKSP, so it is advantageous for the
user to inform NSPCG if it is known beforehand whether
or not the matrix has Property A. In general, finite
element matrices do not have point Property A. If a
5-point central finite difference stencil is used on
a two-dimensional self-adjoint PDE, or if a 7-point
central finite difference stencil is used on a three-
dimensional self-adjoint PDE, the resulting matrix has
Property A. [Default: 2]
- IPARM(19)
- (KBLSZ):
KBLSZ is the 1-D block size. It is used in the
line preconditioners. KBLSZ is the largest integer such
that, if matrix A is considered as a block matrix,
the diagonal blocks have dense bands. [Default: -1]
- IPARM(20)
- (NBL2D):
NBL2D is the 2-D block size. It is used only for the
CGCR acceleration, which is applied to 3-D problems on
a box domain. [Default: -1]
- IPARM(21)
- (IFCTV):
IFCTV is a switch for indicating whether a scalar or a
vectorized routine is to be used for the incomplete
factorization of a matrix stored in symmetric or
nonsymmetric diagonal storage mode. The vectorized
routine should perform better for matrix factorization
patterns which have Property A. [Default: 1]
| 0 |
use scalar routine |
| 1 |
use vectorized routine (default) |
- IPARM(22)
- (IQLR):
IQLR specifies the orientation of the basic preconditioner.
The value of IQLR can be in the range 0 to 3.
[Default: 1]
| 0 |
no basic preconditioner |
| 1 |
left preconditioning (default) |
| 2 |
right preconditioning |
| 3 |
split preconditioning |
- IPARM(23)
- (ISYMM):
ISYMM is a symmetry switch for the matrix. It is used
only for the primary format. If the matrix is symmetric,
a considerable savings in storage is possible if a
factorization preconditioner is called. ISYMM can assume
the following values on input:
| 0 |
matrix is symmetric |
| 1 |
matrix is nonsymmetric |
| 2 |
it is unknown if the matrix is symmetric; NSPCG
should determine if the matrix is symmetric or not
(default) |
If ISYMM = 2 and NSTORE = 1 on input, ISYMM is set to
0 or 1 on output. [Default: 2]
- IPARM(24)
- (IELIM):
IELIM is a switch for effectively removing rows and columns
when the diagonal entry is extremely large compared to the
nonzero off-diagonal entries in that row. See the description
for TOL [= RPARM(15)] for additional details.
[Default: 0]
| 0 |
test not done |
| 1 |
test done for removal of rows and columns |
- IPARM(25)
- (NDEG):
NDEG specifies the degree of the polynomial preconditioner.
[Default: 1]
Description of RPARM parameters
- RPARM(1)
- (ZETA):
ZETA is the stopping test value or approximate relative
accuracy desired in the final computer solution. Iteration
terminates when the stopping test is less than ZETA. If
the method does not converge in ITMAX iterations, ZETA is
reset to an estimate of the relative accuracy achieved.
[Default: 10-6]
- RPARM(2)
- (EMAX):
EMAX is an eigenvalue estimate of the preconditioned matrix
Q-1A. In the SPD case, EMAX is an estimate of the largest
eigenvalue of Q-1A. In the nonsymmetric case, EMAX is an
estimate of the 2-norm of Q-1A. EMAX contains on output
a final adapted value if MAXADP = 1 and the acceleration allows
estimation of eigenvalues. [Default: 2.0]
- RPARM(3)
- (EMIN):
EMIN is an eigenvalue estimate of the preconditioned matrix
Q-1A. In the SPD case, EMIN is an estimate of the smallest
eigenvalue of Q-1A. In the nonsymmetric case, EMIN is an
estimate of the 2-norm of the inverse of Q-1A.
EMIN contains on output a final adapted value if
MINADP = 1 and the acceleration allows estimation of
eigenvalues. [Default: 1.0]
- RPARM(4)
- (FF):
FF is an adaptive procedure damping factor for the estimation
of OMEGA for the SSOR methods. Its values lie in the interval
(0,1] with 1.0 causing the most frequent parameter
changes when IOMGAD = 1 is specified. [Default: 0.75]
- RPARM(5)
- (FFF):
FFF is an adaptive procedure damping factor for changing
EMAX and EMIN in the Chebyshev accelerations (SI and SRSI).
Its values lie in the interval (0,1] with 1.0 causing the
most frequent parameter changes when MAXADP = 1 and
MINADP = 1 are specified. [Default: 0.75]
- RPARM(6)
- (TIMIT):
TIMIT on output is the iteration time in seconds of the
NSPCG call. The iteration time includes the time to perform
all the iterations, including the time to perform the
stopping test. [Default: 0.0]
- RPARM(7)
- (DIGIT1):
DIGIT1 is one measure of the approximate number of digits
of accuracy of the solution. DIGIT1 is computed as the
negative of the logarithm base 10 of the final value
of the stopping test. [Default: 0.0]
- RPARM(8)
- (DIGIT2):
DIGIT2 is the approximate number of digits of accuracy
using the estimated relative residual with the final
approximate solution. DIGIT2 is computed as the negative
of the logarithm base 10 of the ratio of the 2-norm
of the residual vector and the 2-norm of the right-hand-side
vector. This estimate is unrelated to the condition
number of the original system and therefore it will not
be accurate if the system is ill-conditioned.
[Default: 0.0]
Note: DIGIT1 is determined from the actual stopping test
computed on the final iteration, whereas DIGIT2 is based
on the computed residual vector using the final approximate
solution after the algorithm has terminated. If these
values differ greatly, then either the stopping test has
not worked successfully or the original system is
ill-conditioned.
- RPARM(9)
- (OMEGA):
OMEGA serves two purposes:
- 1.
- It is the overrelaxation parameter
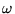 for the SOR
and SSOR methods. OMEGA contains on output a final
adapted value if IOMGAD = 1 is specified and the
acceleration allows estimation of
for the SOR
and SSOR methods. OMEGA contains on output a final
adapted value if IOMGAD = 1 is specified and the
acceleration allows estimation of 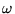 (SOR, SRCG, and
SRSI only). Otherwise, OMEGA is not changed and the
fixed value of OMEGA is used throughout the iterations.
(SOR, SRCG, and
SRSI only). Otherwise, OMEGA is not changed and the
fixed value of OMEGA is used throughout the iterations.
- 2.
- It can be used in the modified incomplete factorization
methods (both point and block) to specify a degree of
modification. In the unmodified incomplete
factorization method, a factor element is discarded
if it results in fill-in outside the prespecified
fill-in region (determined by LVFILL). In the
modified incomplete factorization method, that factor
element is added to the diagonal element of the row
in which it would have caused the fill-in. OMEGA
can be used to indicate that
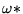 (factor element)
should be added to the diagonal element instead, where
(factor element)
should be added to the diagonal element instead, where
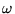 lies in the interval [0,1]. Thus,
lies in the interval [0,1]. Thus, 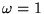 corresponds
to full modification and
corresponds
to full modification and 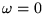 corresponds to no
modification. This facility is useful, for example,
when the IC (ILU) factorization of a matrix exists,
but the MIC (MILU) factorization does not. Then a
value of
corresponds to no
modification. This facility is useful, for example,
when the IC (ILU) factorization of a matrix exists,
but the MIC (MILU) factorization does not. Then a
value of 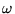 between 0 and 1 can be chosen
with one
of the preconditioners MIC, MBIC, or MBICX to get
a stronger factorization than IC, BIC, or BICX,
respectively.
between 0 and 1 can be chosen
with one
of the preconditioners MIC, MBIC, or MBICX to get
a stronger factorization than IC, BIC, or BICX,
respectively.
[Default: 1.0]
- RPARM(10)
- (ALPHAB):
ALPHAB is an estimate of the minimum eigenvalue of
-D-1(CL+CU) where
A=D-CL-CU for the
SSOR methods. ALPHAB contains on output a final estimated
value if IOMGAD = 1 is specified and the acceleration allows
estimation of ALPHAB (SRCG and SRSI only). ALPHAB only
affects the SSOR and LSSOR preconditioners, and is used in
the adaptive procedure for
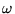 .
[Default: 0.0]
.
[Default: 0.0]
- RPARM(11)
- (BETAB):
BETAB is an estimate of the maximum eigenvalue of
D-1CLD-1CU where
A=D-CL-CU for the SSOR
methods. BETAB contains on output a final estimated value
if IOMGAD = 1 is specified and the acceleration allows
estimation of BETAB (SRCG and SRSI only). BETAB only
affects the SSOR and LSSOR preconditioners, and is used in
the
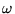 adaptive procedure. [Default: 0.25]
adaptive procedure. [Default: 0.25]
- RPARM(12)
- (SPECR):
SPECR is an estimate of the spectral radius of the SOR
iteration matrix. SPECR contains on output a final
estimated value if IOMGAD = 1 is specified and the
acceleration allows estimation of SPECR (SOR only).
SPECR only affects the SOR and LSOR preconditioners, and
is used in the
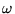 adaptive procedure. [Default: 0.0]
adaptive procedure. [Default: 0.0]
- RPARM(13)
- (TIMFAC):
TIMFAC on output is the factorization time in seconds
required in the NSPCG call. [Default: 0.0]
- RPARM(14)
- (TIMTOT):
TIMTOT on output is the total time in seconds for the
NSPCG call. TIMTOT = TIMFAC + TIMIT + other where
``other" includes scaling and permuting, if requested.
[Default: 0.0]
- RPARM(15)
- (TOL):
TOL is a tolerance factor used for eliminating certain
equations when IELIM = 1 is selected. In that case,
rows are eliminated for which the ratio of the sum of
the absolute values of the off-diagonal elements to the
absolute value of the diagonal element is small (less
than TOL). This is done by dividing the right-hand-side
entry for that equation by the diagonal entry, setting
the diagonal entry equal to one, and setting the
off-diagonal entries of that row to zero. The off-diagonal
entries of the corresponding column are also set to zero
after correcting the right-hand-side vector. This
procedure is useful for linear systems arising from
finite element discretizations of partial differential
equations in which Dirichlet boundary conditions are
handled by penalty methods (giving the diagonal values
of the corresponding equations extremely large values).
(The installer of this package should set the value of
SRELPR. See comments in the Installation Guide in
Section 18 for additional details.)
[Default: 500*SRELPR]
- RPARM(16)
- (AINF):
AINF is the infinity norm of the matrix A if the LSP
preconditioner is used and the infinity norm of
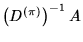 if the LLSP preconditioner is used.
These preconditioners are only effective if the matrix
is SPD or nearly so. If the user does not overwrite
the default value, zero, the program attempts to calculate
a value for this quantity. [Default: 0.0]
if the LLSP preconditioner is used.
These preconditioners are only effective if the matrix
is SPD or nearly so. If the user does not overwrite
the default value, zero, the program attempts to calculate
a value for this quantity. [Default: 0.0]
Table 2:
Default Values for IPARM Variables
The default values for the IPARM and RPARM variables are
given in the tables below.
| Position |
Name |
Default |
| IPARM(1) |
NTEST |
2 |
| IPARM(2) |
ITMAX |
100 |
| IPARM(3) |
LEVEL |
0 |
| IPARM(4) |
NOUT |
6 |
| IPARM(5) |
IDGTS |
0 |
| IPARM(6) |
MAXADP |
1 |
| IPARM(7) |
MINADP |
1 |
| IPARM(8) |
IOMGAD |
1 |
| IPARM(9) |
NS1 |
5 |
| IPARM(10) |
NS2 |
100000 |
| IPARM(11) |
NS3 |
0 |
| IPARM(12) |
NSTORE |
2 |
| IPARM(13) |
ISCALE |
0 |
| IPARM(14) |
IPERM |
0 |
| IPARM(15) |
IFACT |
1 |
| IPARM(16) |
LVFILL |
0 |
| IPARM(17) |
LTRUNC |
0 |
| IPARM(18) |
IPROPA |
2 |
| IPARM(19) |
KBLSZ |
-1 |
| IPARM(20) |
NBL2D |
-1 |
| IPARM(21) |
IFCTV |
1 |
| IPARM(22) |
IQLR |
1 |
| IPARM(23) |
ISYMM |
2 |
| IPARM(24) |
IELIM |
0 |
| IPARM(25) |
NDEG |
1 |
|
Table 3:
Default Values for RPARM Variables
| Position |
Name |
Default |
| RPARM(1) |
ZETA |
10-6 |
| RPARM(2) |
EMAX |
2.0 |
| RPARM(3) |
EMIN |
1.0 |
| RPARM(4) |
FF |
0.75 |
| RPARM(5) |
FFF |
0.75 |
| RPARM(6) |
TIMIT |
0.0 |
| RPARM(7) |
DIGIT1 |
0.0 |
| RPARM(8) |
DIGIT2 |
0.0 |
| RPARM(9) |
OMEGA |
1.0 |
| RPARM(10) |
ALPHAB |
0.0 |
| RPARM(11) |
BETAB |
0.25 |
| RPARM(12) |
SPECR |
0.0 |
| RPARM(13) |
TIMFAC |
0.0 |
| RPARM(14) |
TIMTOT |
0.0 |
| RPARM(15) |
TOL |
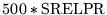 |
| RPARM(16) |
AINF |
0.0 |
|




Next: Storage Modes
Up: NSPCG User's Guide
Previous: Brief Background on Accelerators
