M408M Learning Module Pages
Main page

Astronomy

Kepler's laws say that planets follow elliptical orbits around the sun, with the sun at a focus. In other words, the distance $r$ between a planet and the sun is given by $$r = \frac{ed}{1-e\cos(\theta-\theta_0)}.$$

Perihelion and Aphelion: The point $\theta=\theta_0+\pi$ where the planet is closest to the sun is called perihelion, and is at distance $\displaystyle{r = \frac{ed}{1+e}}$. The point $\theta=\theta_0$ where the planet is farthest from the sun is called aphelion, and is at distance $\displaystyle{r=\frac{ed}{1-e}}$. (The terms perihelion and aphelion come from the Greek word helios, meaning sun, and are only applied to orbits around the sun.)

Most planets have very low eccentricity, and their orbits are almost circles. The earth's eccentricity is only 0.0167, or 1.67%, so the distance to the sun at aphelion (around July 4) is about 3.3% farther than at perihelion (around January 3). As a result, the earth receives about 6.5% more sunlight in January than in July! [Note: seasons are caused by the tilt of the earth's axis, not by the eccentricity of the orbit.]

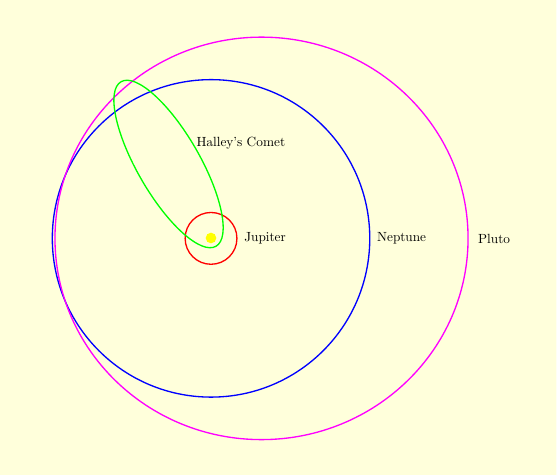
A few planets are a bit more eccentric. Mercury's eccentricity is about .2056. Pluto, no longer considered a planet, has an eccentricity of .248. At perihelion, Pluto is closer to the sun than Neptune. At aphelion, it is 60% farther.

Comets have very high eccentricity, close to 1. They start very far from the sun, plunge into the solar system, make a close pass, and then zip out again. Halley's Comet has an eccentricity of .967, meaning that at aphelion it is $\displaystyle{\frac{1+e}{1-e}\approx 60}$ times farther from the sun than at perihelion. Comet Hale-Bopp, the brightest comet ever seen when it passed the sun in 1997, had an eccentricity of .995. Its aphelion is about 400 times farther than its perihelion.

Occasionally, a comet will get a gravitational kick from a planet as it enters the solar system. This extra energy gives it an eccentricity slightly greater than 1. Comet C/1980 E1 had an eccentricity of 1.057. It followed a hyperbolic trajectory out of the solar system, and will never return.

Chapter 10: Parametric Equations and Polar Coordinates

Learning module LM 10.1: Parametrized Curves:

Learning module LM 10.2: Calculus with Parametrized Curves:

Learning module LM 10.3: Polar Coordinates:

Learning module LM 10.4: Areas and Lengths of Polar Curves:

Learning module LM 10.5: Conic Sections:

Learning module LM 10.6: Conic Sections in Polar Coordinates:

Chapter 12: Vectors and the Geometry of Space

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Astronomy