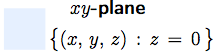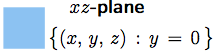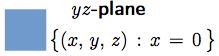M408M Learning Module Pages
Main page

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

       Rectangular coordinates in $3$-space
      Rectangular coordinates in $3$-space p2
      Terminology and notation

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of lines and planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Rectangular coordinates in $R^3$

Rectangular Coordinates in $3$-space

 

Calculus for functions $z = f(x,\,y)$ of two (or more) variables relies heavily on what you already know about the calculus of functions $y = f(y)$ of one variable. Since the graph of a function $z = f(x,\, y)$ of a function of two variables is a surface in $3$-space we'll have to introduce suitable coordinate systems in $3$-space. The first one is the Cartesian $xyz$-coordinate system obtained by adding the $ z$-axis perpendicular to the usual $ xy$-coordinate system in the $xy$-plane.

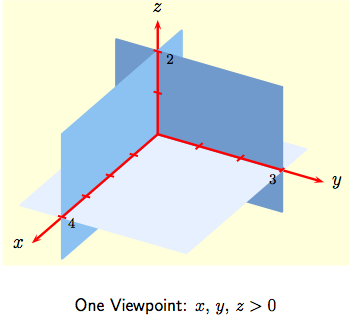
    Each point $P$ in $3$-space is determined by a triple $(a,\, b,\, c)$ as shown to the right. The three coordinate axes intersect at the origin, and each pair of axes determines a coordinate plane. The $x$- and $y$-axes determine the $xy$-plane shown in light blue, for example.
If we drop a perpendicular from $P$ to the the $xy$-plane, we get a point $Q$ with coordinates $(a,\,b,\, 0)$ called the projection of $P$ on the $xy$-plane. In the same way there are projections $R(0,\,b,\,c)$ and $S(a,\,0,\,c)$ of $P$ on the $yz$-plane and $zx$-plane respectively.

The figures below show the three coordinate planes from two viewpoints :

Colors and algebraic descriptions help identify the coordinate planes (remember these algebraic descriptions!):

Because the coordinate axes are mutually perpendicular, this coordinate system is often referred to as the rectangular coordinate system for 3-space. Shortly, we'll introduce other useful coordinate systems for 3-space, extending polar coordinates in the $xy$-plane.

  Example 1: find the distance of the point $P(5,\,4,\, 7)$ from the plane $z = 3$.

Solution: the plane $z = 3$ shown in green is parallel to the plane $z = 0$, in other words to the $xy$-plane. It consists of all points with coordinates $(x,\,y,\, 3)$. So its graph is the one shown to the right, and $P$ lies above the plane $z = 3$. The distance of $P(5,\,4,\,7)$ from the plane $z = 3$ is the length of the dark blue line. Thus $$\hbox{distance}\{(5,\, 4,\, 7), \, z=3\} \ = \ 7 - 3 \ = \ 4 \,.$$