
Home
The Six Pillars of Calculus
The Pillars: A Road MapA picture is worth 1000 words
Trigonometry Review
The basic trig functionsBasic trig identities
The unit circle
Addition of angles, double and half angle formulas
The law of sines and the law of cosines
Graphs of Trig Functions
Exponential Functions
Exponentials with positive integer exponentsFractional and negative powers
The function $f(x)=a^x$ and its graph
Exponential growth and decay
Logarithms and Inverse functions
Inverse FunctionsHow to find a formula for an inverse function
Logarithms as Inverse Exponentials
Inverse Trig Functions
Intro to Limits
Close is good enoughDefinition
One-sided Limits
How can a limit fail to exist?
Infinite Limits and Vertical Asymptotes
Summary
Limit Laws and Computations
A summary of Limit LawsWhy do these laws work?
Two limit theorems
How to algebraically manipulate a 0/0?
Limits with fractions
Limits with Absolute Values
Limits involving Rationalization
Limits of Piece-wise Functions
The Squeeze Theorem
Continuity and the Intermediate Value Theorem
Definition of continuityContinuity and piece-wise functions
Continuity properties
Types of discontinuities
The Intermediate Value Theorem
Examples of continuous functions
Limits at Infinity
Limits at infinity and horizontal asymptotesLimits at infinity of rational functions
Which functions grow the fastest?
Vertical asymptotes (Redux)
Toolbox of graphs
Rates of Change
Tracking changeAverage and instantaneous velocity
Instantaneous rate of change of any function
Finding tangent line equations
Definition of derivative
The Derivative Function
The derivative functionSketching the graph of $f'$
Differentiability
Notation and higher-order derivatives
Basic Differentiation Rules
The Power Rule and other basic rulesThe derivative of $e^x$
Product and Quotient Rules
The Product RuleThe Quotient Rule
Derivatives of Trig Functions
Two important LimitsSine and Cosine
Tangent, Cotangent, Secant, and Cosecant
Summary
The Chain Rule
Two forms of the chain ruleVersion 1
Version 2
Why does it work?
A hybrid chain rule
Implicit Differentiation
Introduction and ExamplesDerivatives of Inverse Trigs via Implicit Differentiation
A Summary
Derivatives of Logs
Formulas and ExamplesLogarithmic Differentiation
Derivatives in Science
In PhysicsIn Economics
In Biology
Related Rates
OverviewHow to tackle the problems
Example (ladder)
Example (shadow)
Linear Approximation and Differentials
OverviewExamples
An example with negative $dx$
Differentiation Review
Basic Building BlocksAdvanced Building Blocks
Product and Quotient Rules
The Chain Rule
Combining Rules
Implicit Differentiation
Logarithmic Differentiation
Conclusions and Tidbits
Absolute and Local Extrema
DefinitionsThe Extreme Value Theorem
Fermat's Theorem
How-to
The Mean Value and other Theorems
Rolle's TheoremsThe Mean Value Theorem
Finding $c$
$f$ vs. $f'$
Increasing/Decreasing Test and Critical NumbersHow-to
The First Derivative Test
Concavity, Points of Inflection, and the Second Derivative Test
Indeterminate Forms and L'Hospital's Rule
What does $\frac{0}{0}$ equal?Indeterminate Differences
Indeterminate Powers
Three Versions of L'Hospital's Rule
Proofs
Optimization
StrategiesAnother Example
Newton's Method
The Idea of Newton's MethodAn Example
Solving Transcendental Equations
When NM doesn't work
Anti-derivatives
Anti-derivatives and PhysicsSome formulas
Anti-derivatives are not Integrals
The Area under a curve
The Area Problem and ExamplesRiemann Sums Notation
Summary
Definite Integrals
DefinitionProperties
What is integration good for?
More Examples
The Fundamental Theorem of Calculus
Three Different QuantitiesThe Whole as Sum of Partial Changes
The Indefinite Integral as Antiderivative
The FTC and the Chain Rule
The Area Problem and Examples
Integration is a process for computing bulk quantities by estimating
and adding up smaller pieces. The mantra (and the 5th Pillar of Calculus) is:
| the whole is the sum of the parts |
The idea works in many different settings. In this learning module we will develop the simplest application of integration, namely finding the area under a curve.
Example 1: Find the area under the curve $y=2$ and above the
$x$-axis between $x=1$ and $x=4$.
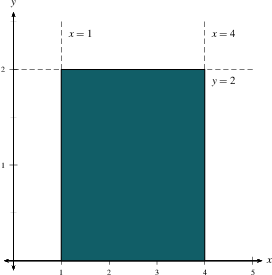
Solution: The region is just a rectangle. The height of the rectangle is $2$, and the width is $4-1=3$, so the area is 6. |
Example 2: Find the approximate area under the curve $y=f(x)$
and above the $x$ axis between $x=1$ and $x=4$,
where $f(x) = 2 + 0.02 x$.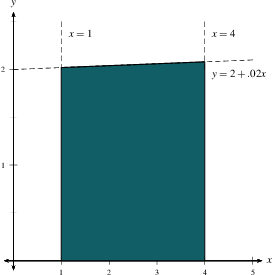
Solution: This is almost the same problem, except that the height of the curve isn't constant. Even so, the height doesn't change much between $x=1$ and $x=4$, so we can replace the curve $y=f(x)$ with the horizontal line $y=f(1)$ to get an approximate total area of $(4-1)f(1) = 3(2.02)=6.06$. |
The answer in Example 2 is a little bit too small, since the curve goes up from $y=2.02$ at $x=1$ to $y=2.08$ at $x=4$. If we wanted an overestimate of the area, we would use the value of $f(x)$ at the right endpoint instead: $(4-1)f(4)=3(2.08)=6.24$. And if we wanted a more accurate guess, we might use the midpoint $f(2.5)=2.05$ and estimate the area as $(4-1)f(2.5)=3(2.05)=6.15$. But whether you use the left endpoint, the right endpoint, or the midpoint, you get roughly the same answer, since the function just isn't changing very much between $x=1$ and $x=4$.
So how do you find the area under a curve that is changing a lot? For instance, how would you find the area under $y=x^2$ between $x=-1$ and $x=1$? The answer is to break the interval $[-1,1]$ up into pieces, each so small that the function doesn't change much in that piece. Then add up the pieces to get a good estimate of the total. As with most of calculus, the exact answer is then the limit of these approximate answers.
The animation below shows how this area can be approximated by adding up narrower and narrower rectangles, with $x_i^*$ being the left/mid/right endpoint.
Main Ideas and Examples