Graphing polar functions

Definitions of Polar Coordinates

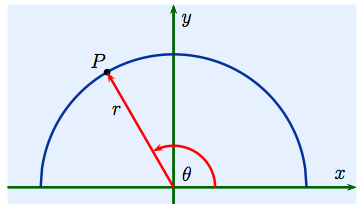
The polar coordinates of the point $P$ shown to the right are written $(r,\, \theta)$ where $r$ is the distance of $P$ from the origin and $\theta$ is the angle the line from the origin to $P$ makes with the $x$ -axis, the angle being measured as $\theta$ rotates counter-clockwise starting from the positive $x$ -axis. At the origin $r= 0$ , but $\theta$ is not well-defined, so we usually assign to the origin the polar coordinates $(0,\, \theta)$ for any choice of $\theta$ .

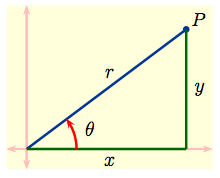
By right-triangle trigonometry and the Pythagorean theorem:

$\sin \theta \ = \ \frac{y}{r}, \quad \cos \theta \ = \ \frac{x}{r}\,, \quad r^2 \ = \ x^2 + y^2\,, \quad \tan \theta \ = \ \frac{y}{x}\,.$ Thus for a point

$P$ the Cartesian and polar coordinate systems are related by

$(x,\, y) \ = \ (r \cos \theta,\, r \sin \theta)\,, \quad (r,\, \theta) \ = \ \left(\sqrt{x^2+y^2},\ \tan^{-1}\Bigl( \frac{y}{x}\Bigr)\right)\,.$

Notice that the choices of coordinates $r$ and $\theta$ are not unique for a given point $P$ since $(r,\, \theta),\ (r,\, \theta +2\pi)$ and $(-r,\, \pi +\theta)$ all describe the same point $P$ .

Chapter 10: Parametric Equations and Polar Coordinates

Learning module LM 10.1: Parametrized Curves:

Learning module LM 10.2: Calculus with Parametrized Curves:

Learning module LM 10.3: Polar Coordinates:

Learning module LM 10.4: Areas and Lengths of Polar Curves:

Learning module LM 10.5: Conic Sections:

Learning module LM 10.6: Conic Sections in Polar Coordinates:

Chapter 12: Vectors and the Geometry of Space

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Graphing polar functions