Main page
Chapter 10: Parametric Equations and Polar Coordinates
Learning module LM 10.1: Parametrized Curves:
Learning module LM 10.2: Calculus with Parametrized Curves:
Learning module LM 10.3: Polar Coordinates:
Learning module LM 10.4: Areas and Lengths of Polar Curves:
Area inside a polar curveArea between polar curves
Arc lengths of polar curves
Learning module LM 10.5: Conic Sections:
Learning module LM 10.6: Conic Sections in Polar Coordinates:
Chapter 12: Vectors and the Geometry of Space
Chapter 13: Vector Functions
Chapter 14: Partial Derivatives
Chapter 15: Multiple Integrals
Area inside a polar curve
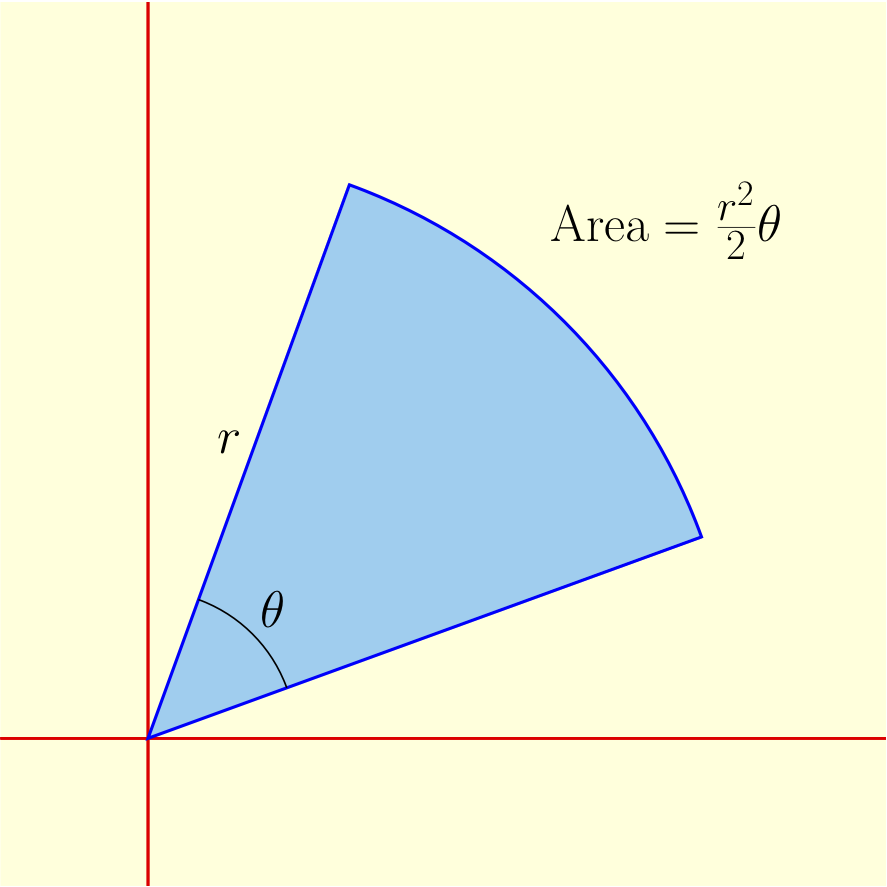
| To understand the area inside of a polar curve $r=f(\theta)$, we start with the area of a slice of pie. If the slice has angle $\theta$ and radius $r$, then it is a fraction $\frac{\theta}{2\pi}$ of the entire pie. So its area is $$\frac{\theta}{2\pi} \pi r^2 = \frac{r^2}{2}\theta.$$ |
|
Now we can compute the area inside of polar curve $r=f(\theta)$
between angles $\theta=a$ and $\theta=b$. As with all bulk
quantities, we
- Break the region into $N$ small pieces.
- Estimate the contribution of each piece.
- Add up the pieces.
- Take a limit to get an integral.
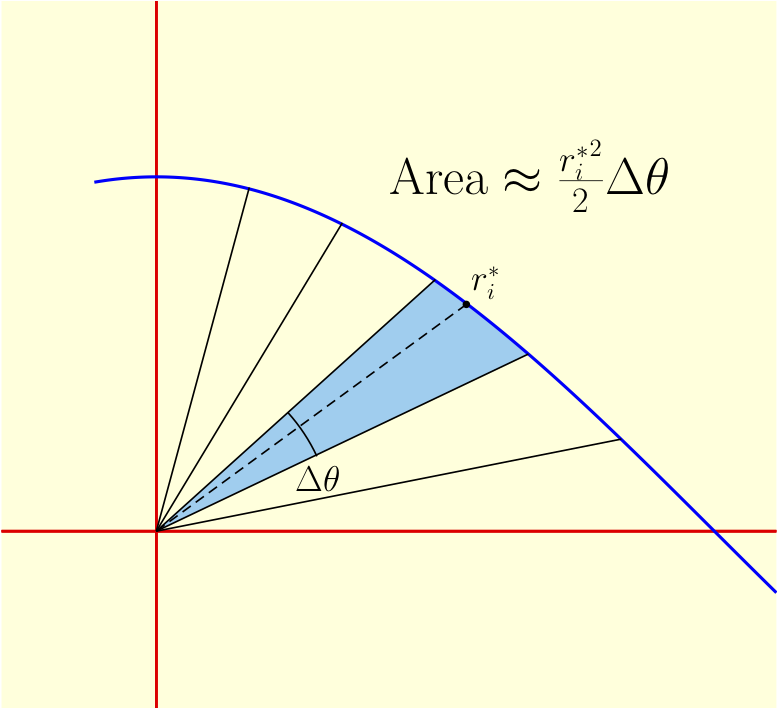
| In our case, the pieces are slices of angle $\Delta \theta = (b-a)/N$. These aren't exactly pie slices, since the radius isn't constant, but it's a good approximation when $N$ is large and $\Delta \theta$ is small. The $i$-th slice has area approximately $f(\theta_i^*)^2 \Delta \theta/2$, where $\theta_i^*$ is a representative angle between $a+(i-1)\Delta \theta$ and $a+i \Delta \theta$, so the whole thing has area approximately $\displaystyle{\sum_{i=1}^N \frac{f(\theta_i^*)^2}{2}\Delta \theta}$. Taking a limit as $N \to \infty$ gives the integral $$\int_a^b \frac{f(\theta)^2}{2} d\theta, \qquad \hbox{or equivalently} \qquad \frac{1}{2}\int_a^b f(\theta)^2 d\theta.$$ |
|
The following video goes over the derivation of this formula, and uses it to compute the area inside one lobe of a cardioid.