Main page
Chapter 10: Parametric Equations and Polar Coordinates
Chapter 12: Vectors and the Geometry of Space
Learning module LM 12.1: 3-dimensional rectangular coordinates:
Learning module LM 12.2: Vectors:
Learning module LM 12.3: Dot products:
Learning module LM 12.4: Cross products:
Learning module LM 12.5: Equations of Lines and Planes:
Learning module LM 12.6: Surfaces:
Surfaces and tracesLevel curves
Level surfaces
Worked problems
Chapter 13: Vector Functions
Chapter 14: Partial Derivatives
Chapter 15: Multiple Integrals
Level surfaces
Now let's step up a dimension and consider functions $w=f(x,\,y,\,z) : U \subseteq {\mathbb R}^3 \to {\mathbb R}$ of $3$ variables; one such function is $${\color{darkerblue} w \ = \ f(x,\,y,\, z) \ = \ x^2 + y^2 - z^2\,.}$$ The graph of every function $w = f(x,\,y,\, z)$ will be a surface in ${\mathbb R}^4$, though it can't be drawn directly; however, slicing horizontally by $w = c$ produces relations $c = f(x,\,y,\, z)$ in $x,\, y,$ and $z$ whose graphs will be surfaces in $3$-space which can be drawn. Formally,
| Level surfaces: For a function $w=f(x,\,y,\,z) :\, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteq {\mathbb R}^3 $ on which $f\Bigl|_{S} = c\, $. |
Example 1: The graph of $z=f(x,\,y)$ as a surface in $3$-space can be regarded as the level surface $w = 0$ of the function $w(x,\,y,\,z) = z - f(x,\, y)$.
Example 2: Spheres $x^2+y^2+z^2 = r^2$ can be interpreted as level surfaces $w = r^2$ of the function $w = x^2+y^2+z^2$. Can you see how to interpret ellipsoids in the same way?
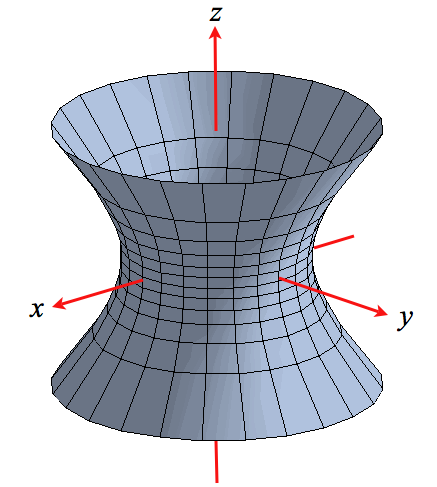
From the earlier example of $ w = f(x,\,y,\, z) = x^2 + y^2 - z^2$. we obtain three particularly important surfaces as level surfaces:
|
|
|
|
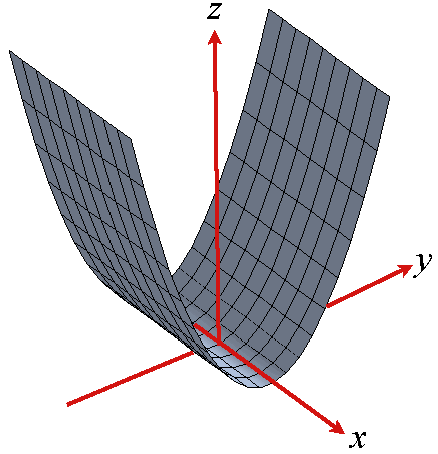
by taking $c = -1,\ 0,$ and $1$. The two-sheeted hyperboloid and double cone are very important in physics, while the single sheeted hyperboloid is a favorite architectural device - cooling towers etc - as is the hyperbolic paraboloid.
Again we can investigate what happens as these surfaces are sliced by planes parallel to the coordinate planes:
Recognize the curves of intersection? There must be some underlying mathematical theory! To do no more than hint at what that theory might be notice
all the surfaces have been the graph of some quadratic
relation in $x,\, y,$ and $z$ like $z - x^2 + y^2 = 0$ in the case
of a hyperbolic paraboloid or $x^2 + y^2 + z^2 = r^2$ for a
sphere,
all the cross-sections of these surfaces have been
conic sections like parabolas, hyperbolas etc.
In view of the first of these comments we make the following
| Definition: a surface $S$ in $3$-space is said to a Quadric Surface when it is the graph of a quadratic relation in $x,\, y,\, $ and $z$. In particular, all the surfaces described so far are Quadric Surfaces. |
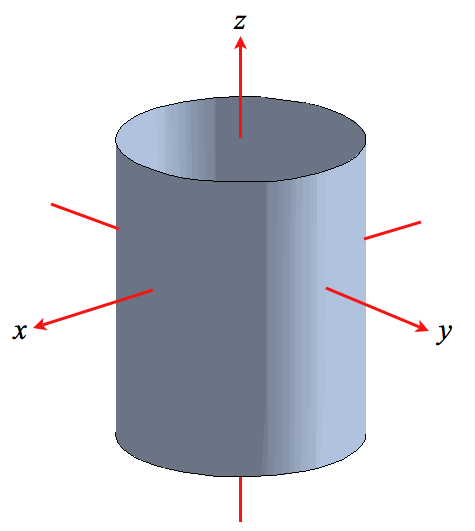
Cylindrical Surfaces: sometimes the intersection of a surface in $3$-space with horizontal planes $z = c$ is the same for all $c$ as in the surface below to the left, or is the same for all vertical planes, say $x = a$, as in the surface to the right.
|
|
|
Do you see that the circular cylinder to the left is the graph in $3$-space of $x^2+ y^2 = r^2$ for fixed $r$ because every horizontal slice is the same circle of radius $r$? Similarly, the cylinder to the right is parabolic; it's the graph of, say, $z = y^2$, since the intersection with every vertical plane $x = a$ is the same parabola $ z = y^2$, say. Not surprisingly, it's called a Parabolic cylinder.