Example problems

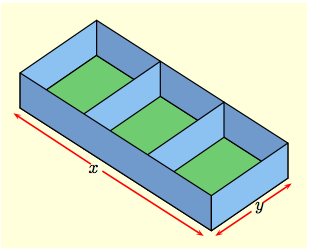
Problem: the rectangular box shown to the right has two parallel partitions but no top. It has a volume of $\,8$ cubic inches.   1. Express the amount, $A$, of material needed to construct the box as a function of the length $x$ and width $y$ of the box (assume no material is wasted).   2. Find the dimensions $x,\, y$ of the box that will require the least amount of material to be used in its construction.

Solution: 1. Let the height of the box be $z$ inches. Then the box has surface area $$A(x,\,y,\,z)\,\,=\,\, xy + 2xz + 4yz$$ because it has no top and two sides in the $x$-direction, while in the $y$-direction it has two parallel partitions as well as two sides. On the other hand, the box has volume $8$ cubic inches, which imposes a constraint condition: $$x y z \,\,=\,\,8, \qquad i.e., \ \ z\,\,=\,\, \frac{8}{xy}\,.$$ Eliminating $z$ from these equations gives $$A(x,\,y)\,\,=\,\, xy + \frac{16}{y}+ \frac{32}{x}\,.$$ This is the surface area as a function of $x,\,y$. We need to find its critical points.

2. By partial differentiation: $$A_x\,\,=\,\,y - \frac{32}{x^2},\qquad\qquad A_y\,\,=\,\, x - \frac{16}{y^2}\,.$$ The critical points of $A$ thus occur when $$y\,\,=\,\, \frac{32}{x^2}, \qquad \qquad x\,\,=\,\, \frac{16}{y^2}\,,$$ i.e., at $(4,\,2)$. At this point $$A\,\,=\,\,A_{xx}\Big|_{(4,2)}\,\,=\,\, \frac{64}{x^3}\Big|_{x=4}\,\,=\,\,1\, > \,0,$$ $$C\,\,=\,\,A_{yy}\Big|_{(4,2)}\,\,=\,\, \frac{32}{y^3}\Big|_{y=2}\,\,=\,\,4\, > \,0,$$ while $$B\,\,=\,\,A_{xy}\Big|_{(4,2)}\,\,=\,\,1\, > \,0\,.$$ Thus $AC - B^2\,>\,0$ at the critical point. Consequently, the surface area is a minimum when $x = 4$ and $y=2$.