$dr = r \; dr \; d\theta$

Conceptually, computing double integrals in polar coordinates is the same as in rectangular coordinates. After all, the idea of an integral doesn't depend on the coordinate system. If $R$ is a region in the plane and $f(x,y)$ is a function, then $\iint_R f(x,y) dA$ is what we get when we

1. Chop $R$ into a bunch of small pieces.
2. Compute $f(x^*,y^*)\Delta A$ for each piece, where $\Delta A$ is the area of the piece.
3. Add up the contributions of the pieces, and
4. Take a limit as we chop $R$ into smaller and smaller pieces.

The differences when working with polar coordinates are explained in the following video:

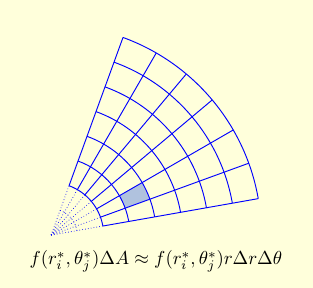
When working with rectangular coordinates, our pieces are boxes of width $\Delta x$, height $\Delta y$, and area $\Delta A = \Delta x \Delta y$. When working with polar coordinates, our pieces are polar rectangles. These are regions of the form $\theta \in [\alpha, \beta]$, $r \in [a,b]$. The approximate contribution of a single box to our integral is $f(r_i^*,\theta_j^*) \Delta A$, where $\Delta A$ is the area of the box. [Here we are thinking of $f$ as a function of $r$ and $\theta$. If $f$ is a function of $x$ and $y$, then strictly speaking we should write $f(r \cos(\theta), r\sin(\theta))$ instead of $f(r,\theta)$.]

So what is the area of a polar rectangle? The polar rectangle is the difference of two pie wedges, one with radius $b$ and one with radius $a$, and so has area \begin{eqnarray*} \Delta A & = & \frac{b^2}{2}(\beta-\alpha) - \frac{a^2}{2}(\beta - \alpha) \\ & = & \frac{b^2-a^2}{2}(\beta-\alpha) \\ & = & \frac{a+b}{2} (b-a)(\beta - \alpha) \\ & = & r^* \Delta r \Delta \theta, \end{eqnarray*} where $\Delta r = b-a$ is the change in $r$ and $\Delta \theta = \beta-\alpha$ is the change in $\theta$.

Another way to understand this is to look at the shape of a small polar rectangle, like the shaded box in the figure above. This is almost a rectangular, only rotated and with slightly curved sides. One side has length $\Delta r$. The other had length approximately $r \Delta \theta$. So the whole rectangle has approximate area $r \Delta r \Delta \theta$.

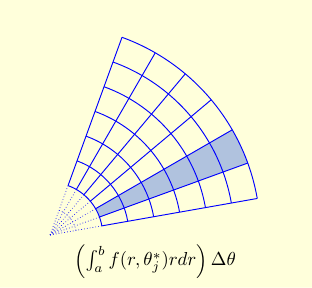
Now we organize our boxes. Since the contribution of each box is approximately $f(r_i^*,\theta_j^*) r_i^* \Delta r \Delta \theta$, the contribution of the boxes in the same thin pie wedge is approximately $\left (\int_a^b f(r,\theta_j^*) r dr \right ) \Delta \theta$.

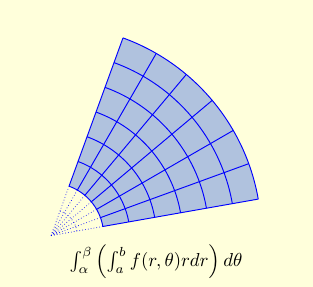
Finally we put all the pie wedges together, to get a total of $\int_{\alpha}^\beta \left ( \int_a^b f(r,\theta) r dr \right ) d\theta$.

The infinitestimal area in rectangular coordinates is $dA = dx\, dy$. The infinitesimal area in polar coordinates is $$dA = r \, dr \, d\theta.$$ Don't forget the factor of $r$!! Double integrals in polar coordinates become iterated integrals $$ \iint f(x,y) dA \ = \ \int\int f(r\cos(\theta), r\sin(\theta)) r \, dr \, d\theta \ = \ \int \int f(r\cos(\theta), r\sin(\theta)) r\, d\theta\,dr,$$ with appropriate limits of integration.