Examples of polar integrals

To compute a double integral $\iint f(x,y) dA$ in polar coordinates, we Rewrite the function $f(x,y)$ in terms of $r$ and $\theta$, Replace $dA$ with $r \, dr\,d\theta$, Compute the limits of integration of $r$. This means finding the minimum and maximum values of $r$ for each value of $\theta$. Compute the limits of integration of $\theta$. These are numbers, not functions of $r$, and Do the iterated integral, one variable at a time.

In our first example, the limits of integration for $r$ do not depend on $\theta$.

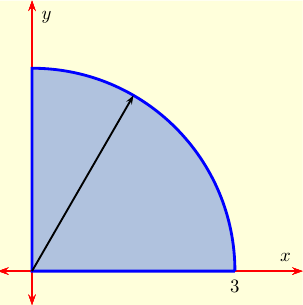
Example 1: Evaluate the integral $$I \ = \ \int \int_D\, (x+y)\, dA$$ when $D$ consists of all points $(x,\,y)$ such that $$0 \ \le \ y \ \le \sqrt{9-x^2}\,, \quad 0\ \le \ x \ \le 3\,.$$ We worked this example in the last section using rectangular coordinates. It is substantially easier in polar coordinates. Our region is the first quadrant inside a circle of radius 3, as shown to the right. This means that our limits of integration are that $r$ goes from 0 to 3 and $\theta$ goes from $0$ to $\pi/2$. Our function is $$f(x,y)\ =\ x+y \ = \ r\cos(\theta) + r\sin(\theta).$$ So the double integral $I$ becomes the iterated integral $$\int_0^{\pi/2}\! \int_0^3 r (\cos(\theta) + \sin(\theta)) r\, dr\, d\theta.$$ For fixed $\theta$, the integral over $r$ is easy: $$\int_0^3 r^2 [\cos(\theta) + \sin(\theta)] dr = 9 [\cos(\theta) + \sin(\theta)].$$

Thus $$I\ = \ \int_0^{\pi/2}\, 9(\cos(\theta)+\sin(\theta)) d\theta \ = \ 18\,.$$ Unlike the integral in rectangular coordinate, there are no square roots and no fancy trig substitutions are required. We just have a simple integral.

When our regions are more complicated than circles, we have to be more careful.

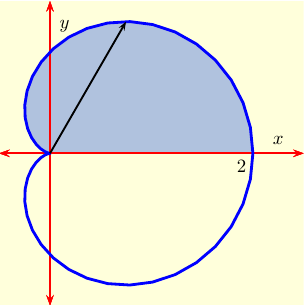
Example 2: Evaluate the integral $$I \ = \ \int \int_D\, y \, dA$$ when $D$ consists of all points above the $x$ axis and inside the cardioid $r = 1+\cos(\theta)$. Our function is $f(x,y) = y = r\sin(\theta)$. For fixed $\theta$, $r$ goes from $0$ to $1 + \cos(\theta)$. Since we are above the $x$ axis, $\theta$ runs from 0 to $\pi$. Thus our double integral becomes the iterated integral $$\int_0^{\pi}\! \int_0^{1+\cos(\theta)} r \sin(\theta) r\, dr\, d\theta.$$ For fixed $\theta$, the integral over $r$ is $$\int_0^{1+\cos(\theta)} r^2 \sin(\theta) dr = \frac{\sin(\theta)(1+\cos(\theta))^3}{3}.$$

Thus \begin{eqnarray*} I & = & \int_0^{\pi}\, \frac{\sin(\theta)(1+\cos(\theta))^3}{3} \, d\theta \\ &=& \left . - \frac{(1+\cos(\theta))^4}{12} \right |_0^\pi \ = \ \frac{4}{3}. \end{eqnarray*}

The function $e^{-x^2}$ does not have an antiderivative that can be expressed in closed form, and it is impossible to compute $\int_{0}^1 e^{-x^2} dx$ exactly. However, the integral $\displaystyle{\int_{-\infty}^\infty e^{-x^2} dx}$ turns out to equal $\sqrt{\pi}.$ In the following video, we use double integrals and polar coordinates to explain this surprising result.