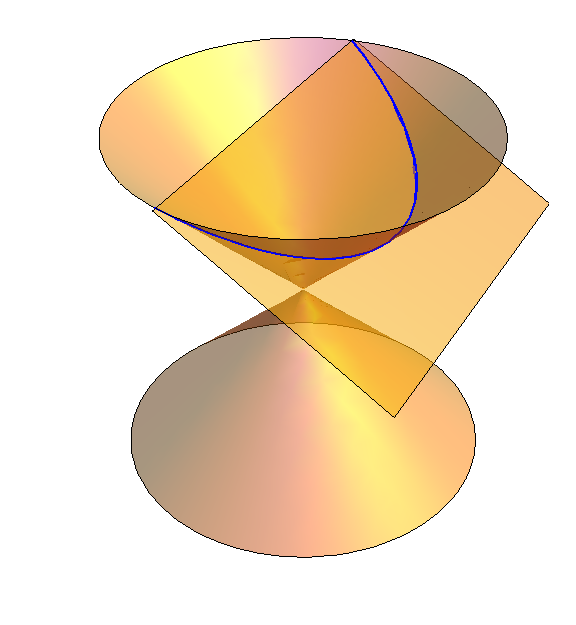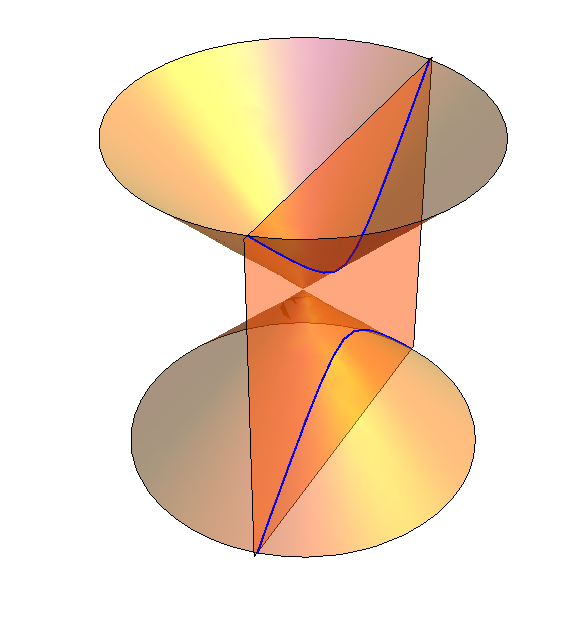Slicing a cone

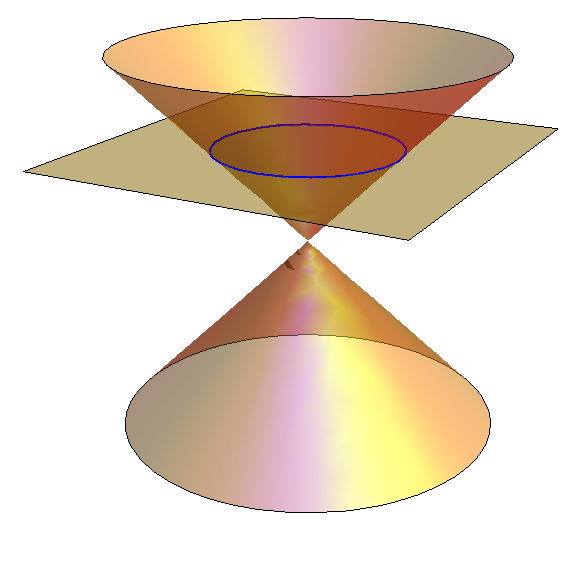
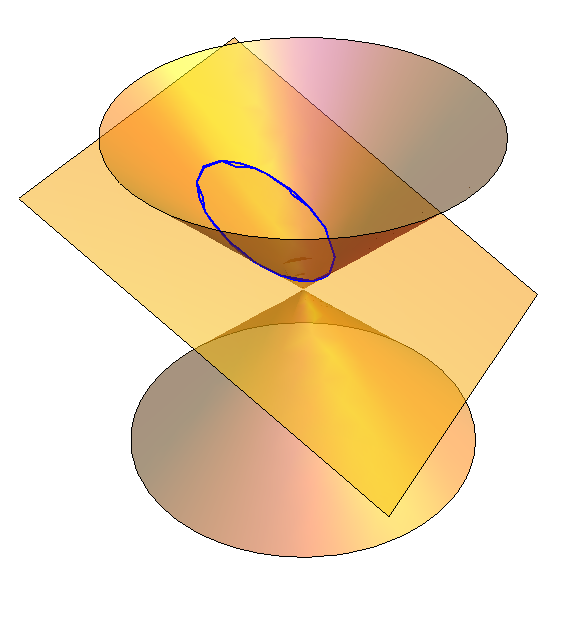
Circles, ellipses, parabolas and hyperbolas are called conic sections. They can all be obtained by slicing the cone $x^2+y^2=z^2$ with a plane.

Example 1: If the plane is horizontal, (say, $z=1$) then we get a circle (say, $x^2+y^2=1$).

Example 2: If the plane is tilted less than 45 degrees, then we get a stretched circle, better known as an ellipse.

Example 3: If the plane is tilted exactly 45 degrees (say, $z=y+1$), then: $$\begin{eqnarray*}y+1 & = & z ,\cr y^2 + 2y + 1 & = & z^2,\cr y^2 + 2y+1 & = & x^2 + y^2, \cr 2y & = & x^2 - 1. \end{eqnarray*}$$ This is a parabola.

Example 4: If the plane is tilted more than 45 degrees, then it hits the cone in two pieces. For instance, if we take the plane $y=1$, then $$\begin{eqnarray*} z^2 & = & x^2 + y^2 ,\cr z^2 & = & x^2 + 1 ,\cr z^2 - x^2 & = & 1.\end{eqnarray*}$$ This is a hyperbola.

Conic sections come up throughout science, and especially in physics and astronomy. If you throw a ball across the room, its trajectory will be a parabola. The earth and other planets move in ellipses around the sun. A comet that has barely enough energy to escape from the sun's gravity will move in a parabolic orbit, and if it has more energy than that, its orbit will be a hyperbola.

[Note: Conic sections can be obtained by slicing any cone with a plane, but the equations come out simplest when we use the 'standard' cone $x^2+y^2=z^2$.]