Main page
Chapter 10: Parametric Equations and Polar Coordinates
Learning module LM 10.1: Parametrized Curves:
Learning module LM 10.2: Calculus with Parametrized Curves:
Learning module LM 10.3: Polar Coordinates:
Learning module LM 10.4: Areas and Lengths of Polar Curves:
Learning module LM 10.5: Conic Sections:
Slicing a coneEllipses
Hyperbolas
Parabolas and directrices
Completing the square
Learning module LM 10.6: Conic Sections in Polar Coordinates:
Chapter 12: Vectors and the Geometry of Space
Chapter 13: Vector Functions
Chapter 14: Partial Derivatives
Chapter 15: Multiple Integrals
Ellipses
Ellipses can be elegantly described in four ways.
|
The simplest description of an ellipse is as a squashed or stretched circle. Start with the unit circle $x^2 + y^2 =1$, and stretch it by a factor of $a$ in the $x$ direction and $b$ in the $y$ direction to get:
| The standard formula for an ellipse in rectangular coordinates is $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.$$ |
|
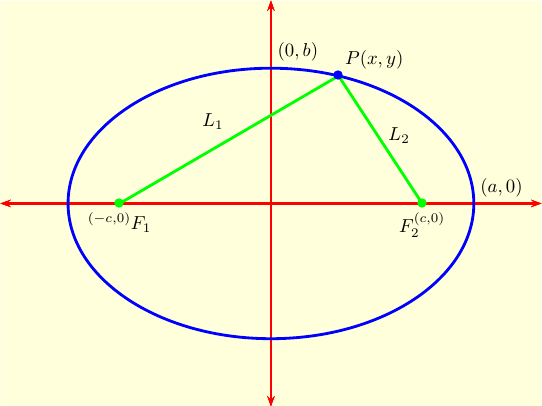
Now let $c = \sqrt{a^2-b^2}$. The points $(\pm c, 0)$ are called foci. These points are extremely important in astronomy, since planets follow elliptical orbits with the sun at a focus, not with the sun at the center. Let $F_1(-c,0)$ and $F_2(c,0)$ be the two foci, let $P(x,y)$ be an arbitrary point on the ellipse. Let $L_1$ be the distance from $F_1$ to $P$, and let $L_2$ be the distance from $F_2$ to $P$, as in the figure on the right. |
|
| Amazing fact: The ellipse is the set of all points where $L_1 + L_2 = 2a$. |
This fact gives elliptical rooms amazing acoustic properties. If you whisper at one focus of such a room, the sound waves from your voice will bounce off the walls and converge at the other focus -- that's why it is called a focus. The same goes for light reflecting off elliptical mirrors.
To understand the amazing fact, let's convert the equation $L_1 + L_2 = 2a$ to rectangular coordinates: \begin{eqnarray*} L_1 + L_2 & = & 2a \cr\cr L_1 & = & 2a-L_2 \cr \cr \sqrt{(x+c)^2+y^2} & = & 2a -\sqrt{(x-c)^2 + y^2} \cr\cr (x+c)^2 + y^2 & = & 4a^2 + (x-c)^2 + y^2 - 4a \sqrt{(x-c)^2 + y^2}\cr\cr 4a\sqrt{(x-c)^2 + y^2}&=& 4a^2-4cx \cr \cr a \sqrt{(x-c)^2 + y^2} &=& a^2-cx \cr \cr a^2(x-c)^2+ a^2 y^2 &=& a^4+c^2x^2 -2a^2cx \cr \cr a^2x^2 + a^2c^2 -2a^2cx + y^2 &=& a^4 + c^2x^2 -2a^2cx \cr \cr (a^2-c^2)x^2 + a^2 y^2 &=& a^2(a^2-c^2) \cr \cr b^2 x^2 + a^2 y^2 &=& a^2b^2 \cr \cr \frac{x^2}{a^2} + \frac{y^2}{b^2} &=& 1,\end{eqnarray*} where we have used the fact that $b^2=a^2-c^2$. That's a long and messy calculation for a simple and elegant result. You should be able to construct the equation of an ellipse given any two of $a$, $b$ and $c$, since you can get the third from $c^2=a^2-b^2.$
|
Example 1: Find the location of the foci of the ellipse
$\displaystyle{\frac{x^2}{25} + \frac{y^2}{9}=1}$.
|
Solution: We have $a=5$ and $b=3$, so $c = \sqrt{a^2-b^2} = 4$. The foci are at $(\pm 4,0)$. |
|
Example 2: Find the equation of an ellipse
with foci at $(\pm 3,0)$ if $b=4$.
|
Solution: Since $c=3$ and $b=4$, $a^2=3^2+4^2=25$, so $a=5$. This makes the equation $$\frac{x^2}{25} + \frac{y^2}{16} = 1.$$ |
|
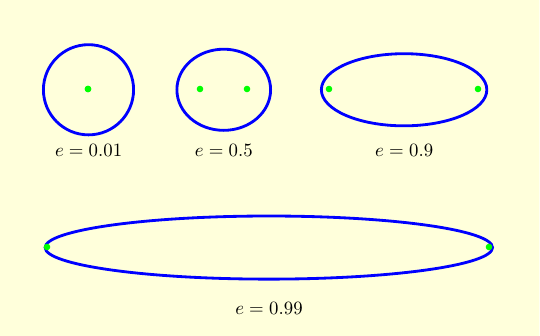
The ratio $c/a$ is called the eccentricity of the ellipse, and is usually denoted $e$. Note that $e < 1$. A circle can be viewed as an ellipse with eccentricity zero, and with both foci at the origin. |
|
| It is easy to plot an ellipse as a parametrized curve. Just take $$x = a \cos(t); \qquad y = b\sin(t),$$ with the parameter $t$ running from $0$ to $2\pi$. |