Hyperbolas

The equations for hyperbolas are very similar to those for ellipses, only with a minus sign.

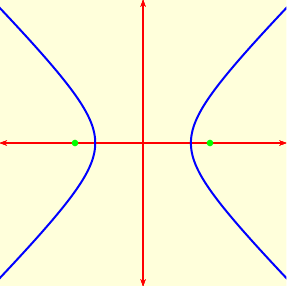
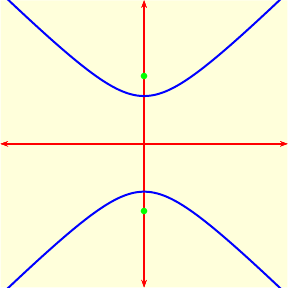
The standard rectangular formulas for hyperbolas are $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$and$$\frac{y^2}{a^2} - \frac{x^2}{b^2}=1.$$The first has foci at $(\pm c, 0)$, where $$c^2 =a^2 + b^2$$ (instead of $a^2-b^2$ for an ellipse), and the second has foci at $(0, \pm c)$. As before, the ratio $c/a$ is called the eccentricity, only now it is bigger than 1.

The hyperbola $x^2-y^2=1$ opens to the sides.

The hyperbola $y^2-x^2=1$ opens up and down.

Hyperbolas can also be described by a distance formula.

Amazing fact for hyperbolas: The hyperbola is the set of all points where $|L_1 - L_2| = 2a$.

(This Amazing Fact can be derived almost exactly the same way that we derived the Amazing Fact for ellipses.)

A hyperbola consists of two pieces, one with $L_1-L_2 = 2a$ and one with $L_1 - L_2 = -2a$. The four ends approach the lines $y = \pm \frac{b}{a}x$ (for the first kind of hyperbola) or $y = \pm \frac{a}{b}x$ (for the second kind). These lines are called asymptotes.

Example: The asymptotes of the hyperbola $x^2 - y^2 = 2$ are the diagonal lines $y = \pm x$. If you rotate this hyperbola counter-clockwise by 45 degrees, you get the curve $y = \frac{1}{x}$, whose asymptotes are the $x$ and $y$ axes.