M408M Learning Module Pages
Main page

Vectors in 2 dimensions

Vectors in 2 Dimensions As a warmup for vectors in 3 dimensions, let's talk about vectors in the plane. (Besides, they're easier to draw!)

What is a vector?:

A vector in the plane is a quantity that has both a magnitude (or length) and a direction, and that can be added to similar quantities. For instance, velocity can be described by a vector because it has a magnitude, namely speed, as well as a direction: the wind blows at a speed of 5 mph from the north-west, Joe heads due north at 75 mph in his car, and so on.

[Note: In higher mathematics, the essential properties of vectors are that they can be rescaled and added to other vectors, and the term vector is used for many things that don't have lengths or directions (e.g., functions). If you take a course in linear algebra or differential equations or quantum mechanics, you'll probably see many examples of this more general idea. For this class, however, it's enough to think of vectors as arrows in the plane or in 3 dimensional space. Our working definition is that, if it has a direction and a length, then it's a vector.]

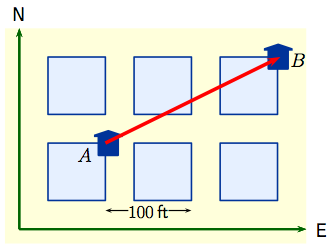
Displacements provide a different type of example: let's look at where Bob lives in relation to Alice. If Alice's house is at point $A$, then Bob's house at point $B$ is $223$ ft. from $A$ in a direction $18^{\circ}$ ENE. If we represent this as an arrow from $A$ to $B$, it determines a vector ${\small\overrightarrow{AB}}$ called a displacement vector with magnitude the distance from $A$ to $B$, and direction the direction from $A$ to $B$. It's natural to represent this vector by an arrow with $A$ the tail and $B$ the head.

In general, we'll usually label vectors by single bold-faced letters like ${\bf a}$, ${\bf v}$, ... , and so on, or by an arrow, as in $\overrightarrow{PQ}$. Beware: physicists and engineers sometimes use different notation. The length of a vector ${\bf v}$ is denoted by $\|{\bf v}\|$ or by $|{\bf v}|$; this length is a positive number except for the zero vector $ {\bf 0 }$ which has length $0$. Of course, not all quantities can be represented as vectors: for instance, mass, temperature and distance have magnitude, but no direction. Such directionless quantities are real numbers $3,\,k,\, \lambda,\, \ldots\, $ and will be referred to as scalars.

Just as for numbers, there are many concepts, algebraic operations and associated properties for vectors.

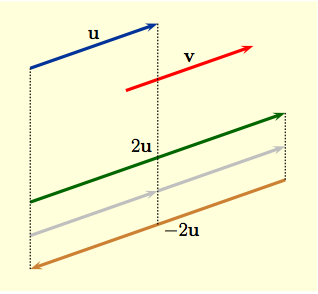
1. Vectors $\bf u$, $\bf v $ shown to the right are said to be equivalent (or equal) because they have the same length and direction even though they are not in the same position.

2. The scalar multiple of a scalar $k$ and vector $\bf v$ is the vector $k {\bf v} $ whose length is $|k|\| {\bf v} \|$; if $k\,>\,0$, then $k {\bf v}$ and ${\bf v}$ have the same direction, while if $k\,<\,0$, then $k{\bf v}$ and ${\bf v}$ point in opposite directions. The examples of $2 {\bf u} $ and $-2 {\bf u} $ to the right show that scalar multiplication really does act as a scaling of a vector.

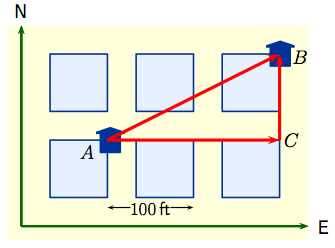
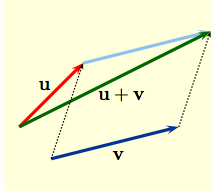
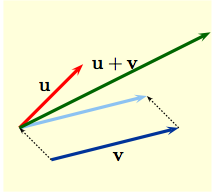
Vectors are said to be parallel when they are scalar multiples of each other. So all the vectors ${\bf u}$, $\bf v$, $2 {\bf u}$ and $-2 {\bf u}$ above are parallel. They surely look parallel!

Although ${\small\overrightarrow{AB}}$ is the displacement vector from Alice's house to Bob's, you can't actually drive across blocks to get there! You might try first going $200$ft. east and then $100$ft. north. In vector terms $$\overrightarrow{AB}\,\,=\,\, \overrightarrow{AC}\,\,+\, \, \overrightarrow{CB},$$ which is just a mathematical way of saying that by adding vectors as indicated, the lengths and directions will get you from $A$ to $B$.

Mathematics doesn't always come in neat rectangular blocks, however! To describe addition of vectors in general, triangles and parallelograms are needed. So let $\bf u $, $\bf v$ be the red and dark blue vectors shown below. The sum ${\bf u} + {\bf v}$ is then the green vector as shown computed by first noting that the dark blue vector is equal to the light blue vector and then applying the respective Triangle and Parallelogram Laws.

move ${\bf v}$ where?
Triangle Law
Parallelogram Law

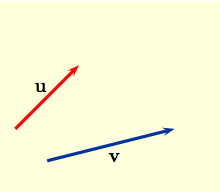
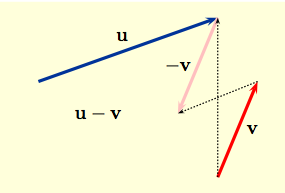
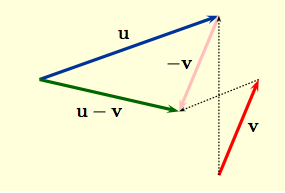
Subtracting is defined by adding $-{\bf v}$; thus the difference ${\bf u} - {\bf v}$ is the sum ${\bf u} + (- {\bf v} $) as shown by

Create ${\bf -v}$ and move it,
then apply the Triangle Law.

To see addition and subtraction of vectors in 'action', check out the interactive version of the figure to the right. Select the ${\bf a} + {\bf b}$ vector. Use the sliders to create several different examples.

(i) Was the triangle or parallelogram law used to create ${\bf a} + {\bf b}$? Why was the vector ${\bf b}$ moved?

(ii) Next create ${\bf b} + {\bf a}$. Does ${\bf b} +{\bf a} = {\bf a} + {\bf b}$? Why?

(iii) Then do the same for ${\bf a} - {\bf b},\, {\bf b} - {\bf a}$. Does ${\bf b} - {\bf a} = {\bf a} - {\bf b}$? Why?

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Vectors in 2 dimensions