Vectors in 2 dimensions

If ${\bf u}$ and ${\bf v}$ are vectors and $a$ and $b$ are numbers, then any vector of the form $a\,{\bf u} + b \,{\bf v}$ is called a linear combination of ${\bf u}$ and ${\bf v}$. Most problems with vectors involve figuring out which vectors are linear combinations of which other vectors, and how.

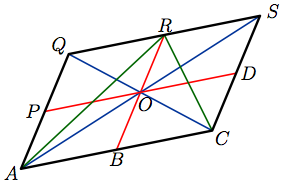
Example 1: when displacement vectors $${\bf u} \ = \ \overrightarrow{AB}\,, \qquad {\bf v} \ = \ \overrightarrow{AP}\,,$$ are specified by the parallelogram express $\overrightarrow{CR}$ in terms of $\bf u$ and $\bf v$.

Solution: By the Parallelogram Law $$\overrightarrow{CR} \ = \ \overrightarrow{CB} +\overrightarrow{CS}\,.$$ But $$\overrightarrow{CB}\ = \ - \overrightarrow{BC}\ = \ - \overrightarrow{AB}\ = \ - {\bf u}\,,$$ while $$\overrightarrow{CS}\ = \ \overrightarrow{AQ}\ = \ 2\,\overrightarrow{AP}\ = \ 2{\bf v}\,.$$ So then $$\overrightarrow{CR} \ = \ 2{\bf v} - {\bf u}\,.$$