M408M Learning Module Pages
Main page

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

       Vectors in 2 dimensions
      Vectors in 2 dimensions p2
      Components and combinations
      On to 3 dimensions

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Components and combinations

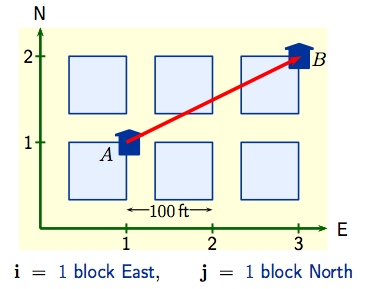
Vectors p4 Coordinates and the unit vectors ${\bf i,\ j}\,$: A very standard way of describing vectors is via basis vectors.

   Instead of saying

Go East $200$ feet and then North $100$ feet,

to get from Alice's house to Bob's, you could say

It's $2$ blocks East and $1$ block North.

Here we're using 'blocks' as a convenient unit. More mathematically, we could introduce the 'unit' vectors $\bf{i}, \ \bf{j}$ and write $$\overrightarrow{AB}\ = \ 2 \bf{i}+ \bf{j}\,.$$

For any two numbers $a$ and $b$, positive or negative, the vector ${\bf v} = a\,{\bf i} + b\,{\bf j}$ makes mathematical sense, because it means that we go $a$ blocks in the East direction and $b$ in the North direction (negative simply means we go backwards). The vector ${\bf v} = a\,{\bf i} + b\,{\bf j}$ is often written $\langle a,\, b\rangle$, and the values of $a,\, b$ are called the components of $\bf v$.

The notation ${\bf v} = a\,{\bf i}+ b\,{\bf j} = \langle a,\, b\rangle$ for vectors is very convenient. For example, addition, subtraction and scalar multiplication are very simple: they are done one variable at a time (also called component-wise): $${\bf u} + {\bf v} \ = \ \langle a_1,\, b_1 \rangle + \langle a_2,\, b_2 \rangle\ = \ \langle a_1+a_2,\, b_1+b_2 \rangle\,, \quad \quad \lambda {\bf w} \ = \ \lambda \langle c,\, d \rangle \ = \ \langle \lambda c,\, \lambda d \rangle\,,$$ while by the Pythagorean theorem, $$ \|{\bf v}\| \ = \ \|a\,{\bf i} + b\,{\bf j}\| \ = \ |\langle \,a,\, b\,\rangle| \ = \ \sqrt{a^2 + b^2}\,.$$ Thus $\|{\bf i}\| = \|\langle 1,\,0\rangle\| = 1 = \|{\bf j}\| \ = \ \|\langle 0,\,1\rangle\| ,$ so ${\bf i},\, {\bf j}$ are 'unit vectors' because they have unit length.

Example 2: Determine $a, \, b$ so that $${\bf u}\ = \ \langle\,-1,\,3\,\rangle $$ is the sum ${\bf u} = a\, {\bf v} + b\, {\bf w}$ of vectors $${\bf v} \,=\, \langle\,-1,\, 2\,\rangle\,, \qquad {\bf w} \,=\, \langle\,1, \,-1 \,\rangle\,. $$
Solution:As addition and scalar multiplication of vectors is done component-wise, 		$${\bf u}\ = \ \langle\,-1,\,3\,\rangle\ = \ a\,\langle\,-1,\,2\,\rangle+ b\,\langle\,1,\,-1\,\rangle $$ $$\qquad = \ \langle\,-a +b,\,2 a - b\,\rangle \ = \ \langle\,-1,\,3\,\rangle\,. $$ Thus $$-a + b \,=\,-1\,, \quad 2a - b\,=\, 3\,.$$ After solving for $a$ and $b$ we get $a \,=\,2,\ b = 1$.


Now that we linked vectors with coordinate axes in the plane, it will turn out to be convenient to introduce displacement vectors whose tail is always at the origin. This identifies points $(a,\,b)$ in the plane with vectors called Position vectors.

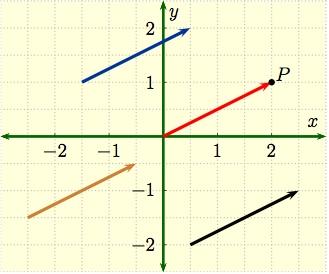
The four vectors to the right are all equivalent because they have the same length and direction; in fact, they are all equivalent to $2{\bf i} + {\bf j}$ since the vector always moves 2 units in the $x$-direction and 1 unit in the $y$-direction.

The red vector with tail at the origin, however, will be called a Position Vector. It identifies the point $P=(2,\, 1)$ in the plane with the vector having tail at the origin and head at $(2,\,1)$. We shall often identify a point $P=(a,\,b)$ with $a\,{\bf i}+b\,{\bf j}$ or $\langle a,\, b\rangle$ as a position vector.