Definitions

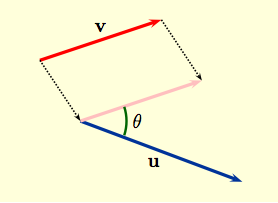
The angle between vectors $\bf u $ and $\bf v $ is the angle $\theta$ shown in the figure to the right by first arranging the vectors so that they have the same tail. Notice that there are really two choices of $ \theta$, one smaller than $ \pi$, the other larger than $\pi$ (unless both equal $\pi$). By convention the smaller one is always chosen, so that $ 0 \, \le \,\theta\, \le \, \pi$. It's important to note that the angle between any two of the unit coordinate vectors $\bf i $, $\bf j $, and $\bf k $ is $\,\frac{1}{2}\pi\,$ because they are mutually perpendicular.

Definition: The Dot Product, ${\bf u}\, {\Large\cdot}\, {\bf v}$, quite frequently called the Inner Product, of vectors $\bf u$ and $\bf v$ is the scalar value defined by $${\bf u} \cdot {\bf v}\ = \ \|{\bf u}\|\|{\bf v}\| \cos \theta$$ where $ \theta $ is the angle between $\bf u$ and $\bf v$. Since $\cos (\frac{1}{2}\pi )\,=\, 0$, vectors ${\bf u}, \, {\bf v}$ are perpendicular when ${\bf u}\cdot {\bf v} \ = \ 0$ and ${\bf u},\, {\bf v} \, \ne\,0$.