Projections and components

02. Dot Products p3 Projections and Components:
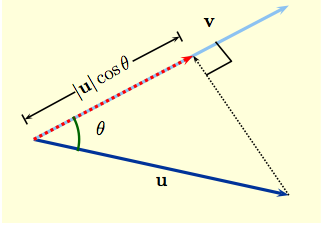
The geometric definition of dot product helps us express the projection of one vector onto another as well as the component of one vector in the direction of another. But let's approach the concept from a different direction: given vectors ${\bf a},\ {\bf b}$ and scalars $\lambda, \ \mu$, we know how to form the linear combination ${\bf u} = \lambda {\bf a} + \mu {\bf b}$ to create a new vector $\bf u$. Suppose instead that we start with vectors ${\bf a},\ {\bf b}$, and a vector $\bf u$. Then we can try to determine scalars $\lambda, \ \mu$ so that $${\bf u} \ = \ \lambda {\bf a} + \mu {\bf b}\,.$$ In mathematical terms, this provides a representation of $\bf u$ in terms of ${\bf a},\ {\bf b}$. It is an extremely important idea that occurs everywhere one tries to model a theoretical or practical situation. (You did something very similar to this with Taylor series, taking for ${\bf a},\ {\bf b}$ the monomials $1,\, x,\, x^2, \, x^3, \, \ldots \ $ and $\bf u$ a function $f(x)$.) The term $ \lambda {\bf a}$ can be thought of as the projection of $\bf u$ on $\bf a$. For simplicity, let's start with just two vectors $\bf u$ and $\bf v$ shown below in dark blue and light blue respectively.

By right triangle trigonometry, the dashed red vector has $$\hbox{length} \ = \ \|{\bf u}\|\cos \theta \ = \ \frac{{\bf u}\cdot{\bf v}}{\|{\bf v}\|}\,,$$ and it points in the direction of $\bf v$. On the other hand, $\displaystyle{\frac{\bf v}{\|\bf v\|}}$ is a unit vector in the direction of $\bf v$. Thus the
$${\color{red}{ \hbox{dashed red vector}}} \ = \ \|{\bf u}\|\cos \theta \left( \frac{\bf v}{\|{\bf v}\|}\right ) \ = \ \left(\frac{{\bf u}\cdot{\bf v}}{\|{\bf v}\|^2}\right){\bf v}\,.$$ Since ${\bf v} \cdot {\bf v} = \|{\bf v}\| \|{\bf v}\| \cos(0) = \|{\bf v}\|^2$, we often write this as $${\color{red}{ \hbox{dashed red vector}}}\ = \ \left (\frac{{\bf u}\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right ) {\bf v}\,.$$

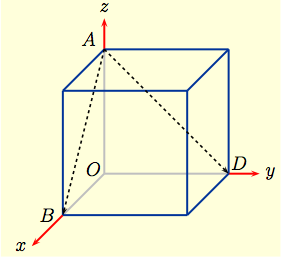
This red vector is called the (vector) projection of $\bf u$ on $\bf v$, written $$ \hbox{proj}_{\bf v} {\bf u} \ = \ \left( \frac{{\bf u} \cdot {\bf v}}{\|{\bf v}\|^2}\right) {\bf v}\, \ = \ \left (\frac{{\bf u}\cdot{\bf v}}{{\bf v}\cdot{\bf v}}\right ) {\bf v}\, ,$$ and its length is called the component of $\bf u$ in the direction of $\bf v$, written $$\hbox{comp}_{\bf v}({\bf u}) \ = \ \left\| \hbox{proj}_{\bf v} {\bf u}\right \| \ = \ \frac{{\bf u}\cdot{\bf v}}{\|{\bf v}\|}\,.$$

Example 3: The box shown in

is the unit cube having one corner at the origin $O$ and the coordinate planes for three of its faces. Determine the projection of $\overrightarrow{AD}$ onto $\overrightarrow{AB}$.

Solution: Since the unit cube has side-length $= 1$, $$A\,=\, (0,\,0,\,1), \ \ B \,=\, (1,\,0,\,0), \ \ D \,=\, (0,\,1,\,0)\,.$$ So when $${\bf u}\ = \ \overrightarrow{AD}\ =\ \langle\,0,\,1,\, -1\,\rangle\,,$$ and $${\bf v}\ = \ \overrightarrow{AB}\ =\ \langle\,1,\, 0,\, -1\,\rangle\,,$$ the projection of ${\small \overrightarrow{AD}}$ on ${\small \overrightarrow{AB}}$ is the vector $$\hbox{proj}_{\bf v}({\bf u}) \ = \ \left(\frac{{\bf u}\cdot{\bf v}}{\|{\bf v}\|^2}\right){\bf v} \ = \ \frac{1}{2}\big\langle\,1,\, 0,\, -1\,\big\rangle\,.$$

Important Special cases: Since the vectors ${\bf i},\, {\bf j},\,$ and $\bf k$ all have unit length, a vector ${\bf v} = \langle\,a,\,b,\,c\,\rangle$ can be written as $${\bf v} \ = \ ({\bf v}\cdot {\bf i})\,{\bf i} + ({\bf v}\cdot {\bf j})\,{\bf j} + ({\bf v}\cdot {\bf k})\,{\bf k} \ = \ a\,{\bf i} + b\,{\bf j} + c\,{\bf k}\,.$$ Components of velocity, or of force vectors like gravity, will be important in this and many other courses.

Directional Angles and Directional Cosines:
A vector ${\bf v} = \langle a, b, c \rangle$ makes an angle $\alpha$ with the $x$-axis, $\beta$ with the $y$-axis, and $\gamma$ with the $z$-axis. The angles $\alpha$, $\beta$, and $\gamma$ are called the directional angles of ${\bf v}$ and $\cos(\alpha)$, $\cos(\beta)$ and $\cos(\gamma)$ are called the directional cosines of ${\bf v}$. Computing directional cosines is easy: $$\cos(\alpha) \ = \ \frac{{\bf v}\cdot {\bf i}}{\|{\bf v}\| \|{\bf i}\|} \ = \ \frac{a}{\sqrt{a^2+b^2+c^2}}.$$Similarly, $$\cos(\beta) \ =\ \frac{b}{\sqrt{a^2+b^2+c^2}}; \qquad \cos(\gamma)\ = \ \frac{c}{\sqrt{a^2+b^2+c^2}}.$$

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Projections and components