M408M Learning Module Pages
Main page

Equations of a line

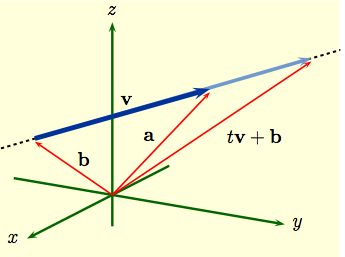
Equations of a Line There are many ways of expressing the equations of lines in $2$-dimensional space. (You probably learned the slope-intercept and point-slope formulas among others.) Now we do the same for lines in $3$-dimensional space. Here vectors will be particularly convenient.
Lines: Two points determine a line, and so does a point and a vector. Imagine a laser pointer at a point ${\bf b}$, and shine it towards another point, say ${\bf a}$. If we extend the beam of the laser pointer in both directions, we get a line.

To write this as an equation, represent the light saber as a displacement vector ${\bf v}$ shown in dark blue, with tail at ${\bf b}$ and head at ${\bf a}$; so ${\bf v} = {\bf a}-{\bf b}$. To extend ${\bf v}$ in both directions we scale the vector by writing $\,t\,{\bf v}$, shown in lighter blue, where $t$ is a real number. Doing this for all such $t$ gives us the complete line. So in vector-form each point on the line is given by $${\bf r}(t) \ = \ t\,{\bf v} + {\bf b}\,.$$ This is similar to the slope-intercept form for a line in the plane. You can also think of the vector form as describing motion with constant velocity, where we start at position ${\bf b}$ at time $t=0$, reach position ${\bf a}$ at time $t=1$, and keep going.

One coordinate at a time: Sometimes it's useful to express the equation for a line in coordinate-form: if we write $${\bf r}(t) \ = \ \langle\,x(t),\, y(t),\, z(t)\,\rangle\,,\qquad {\bf v}\ = \ \langle\,k,\, m,\, n\,\rangle\,,\qquad {\bf b}\ = \ \langle\,x_1,\, y_1,\, z_1\,\rangle\,,$$ then the vector equation becomes $${\bf r}(t) \ = \ t\, {\bf v} + {\bf b} \ = \ \langle\,t k + x_1,\, t m + y_1,\, t n + z_1\,\rangle\,,$$ giving a second equation for a line: $$x(t) \ = \ t k + x_1\,,\qquad y(t) \ = \ t m + y_1\,,\qquad z(t) \ = \ t n + z_1\,.$$ Solving for $t$ in these equations (and writing $x$ instead of $x(t)$ and so on), we then get $$t \,=\,\frac{x-x_1}{k}\,, \qquad t \,=\,\frac{y-y_1}{m}\,, \qquad t \,=\,\frac{z-z_1}{n}\,,$$ giving a third equation $$ \frac{x-x_1}{k}\ = \ \frac{y-y_1}{m}\ = \ \frac{z-z_1}{n}\, .$$ (Actually, this is two equations, since we're setting three things equal to each other. If somebody tells you what $x$ is, you can use one equation to solve for $y$ and the other to solve for $z$. Also, these don't make sense if $k=0$, $m=0$ or $n=0$. If $k$ were zero, then we would still have $\frac{y-y_1}{m}=\frac{z-z_1}{n}$, and we would have $x=x_1$. The other cases are similar.)
The best form for the equation of a line in $3$-space depends on the problem you are trying to solve, but it's often simplest to start with the vector form.

Example 1: Find parametric equations for the line passing through the point $P(4,\,-1,\,3)$ and parallel to the vector $ \bigl\langle\,1,\, 4,\,-3\,\bigl\rangle\,.$

Solution: In vector form a line passing through a point ${\bf b} = \bigl\langle\,4,\,-1,\,3\,\bigl\rangle$ and having direction vector ${\bf v} = \bigl\langle\,1,\, 4,\,-3\,\bigl\rangle $ is given by $${\bf r}(t)\,=\, t{\bf v}+ {\bf b} \,=\, \bigl\langle\,4+t,\, -1+4t,\,3-3t\,\bigl\rangle.$$ This becomes $$x(t)\ = \ 4+t \,, \qquad y(t) \ = \ -1+4t\, \quad$$ $$ z(t) \ = \ 3-3t$$ in parametric form.

Example 2: Find the point of intersection, $P$, of the lines $$\frac{x-2}{4}\ = \ \frac{y-6}{3}\ = \ \frac{z-5}{1}\,,$$ $$\frac{x-4}{2}\ = \ \frac{y-4}{5}\ = \ \frac{z-3}{3}\,.$$ Solution: To determine where the lines intersect it's convenient to convert them to parametric form: $$x=2+4t,\ \ y=6+3t, \ \ z= 5+t\,,$$ $$x=4+2s,\ \ y=4+5s, \ \ z= 3+3s\,.$$ For then the lines intersect when the equations $$2+4t \ = \ 4+2s \,,$$ $$6+3t \ = \ 4+5s\,,$$ $$5+t \ = \ 3+3s\,$$ are satisfied simultaneously. Solving the first two equations gives $t = 1$, $s = 1$, and a check shows that these values then satisfy the third equation.
The lines thus intersect when $s = t = 1$, which if we substitute in the equations for $x,\,y$, and $z$ shows that $$ P \ = \ (6,\ 9, \ 6)\, .$$

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Equations of a line