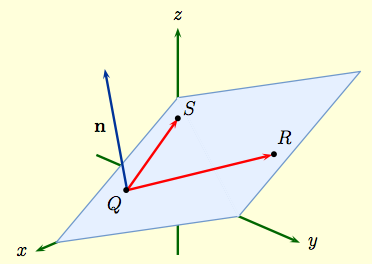
Finding the normal to a plane

Let $${\bf b}=\langle\,x_1,\,y_1,\,z_1\, \rangle\,, \ \ {\bf r} = \langle\,x_2,\,y_2,\,z_2\, \rangle\,, \ \ {\bf s} = \langle\,x_3,\,y_3,\,z_3\, \rangle.$$ The vectors $$\overrightarrow{QR} \ = \ {\bf r} - {\bf b} \,, \qquad \overrightarrow{QS} \ = \ {\bf s} - {\bf b} \,,$$ then lie in the plane. The normal to the plane is given by the cross product ${\bf n} = ( {\bf r} - {\bf b})\times ( {\bf s} - {\bf b})$. Once this normal has been calculated, we can then use the point-normal form to get the equation of the plane passing through $Q,\,R,\,$ and $S$.

Example: Find an equation for the plane passing through the points $$Q(-1,\,1,\,2)\,, \ \ R(-4,\,2,\,2)\,, \ \ S(-2,\,1,\,5)\,.$$     Solution: when the plane passes through $Q,\, R$, and $S$, then the vectors $$\overrightarrow{QR} = \langle\, -3,\, 1,\, 0\, \rangle\,,\qquad \overrightarrow{QS}= \langle\, -1,\, 0,\, 3\, \rangle\,,$$ lie in the plane. Thus the cross-product $${\bf n} \ = \ \left|\begin{array}{ccc}{\bf i} & {\bf j} & {\bf k} \\ -3 & 1 & 0 \\ -1 & 0 & 3 \end{array}\right| \ = \ \ = \ 3{\bf i} +9{\bf j} +{\bf k}$$ is normal to the plane.

If ${\bf r} = \langle \,x,\,y,\, z\,\rangle$ determines an arbitrary point $P$ in the plane, the vector $${\bf v} \ = \ \overrightarrow{QP}\ = \ \langle \,x+1,\,y-1,\, z-2\,\rangle$$ lies in the plane and so is perpendicular to ${\bf n}$. In this case, $${\bf n}\cdot{\bf v}\ = \ 3(x+1) +9(y-1) +(z-2) \ = \ 0\,,$$ which after simplification becomes $$3x +9y +z - 8 \ = \ 0\,.$$ Consequently, the plane $3x +9y +z = 8$ passes through $Q,\, R$, and $S$.