Volumes are double integrals

Double integrals can be viewed as volumes in the same way that we view regular integrals as areas. This cuts two ways. We can compute volumes by doing double integrals. We can also understand double integrals by using what we already know about 3-dimensional geometry!

For $z=f(x,\,y) \ge 0$ and $R$ is a rectangle in the $xy$-plane, then the Double Integral $$ \int\int_R\, f(x,\,y)\, dx dy $$ of $f$ over $R$ equals the volume of the solid under the graph of $f$ and above $R$.

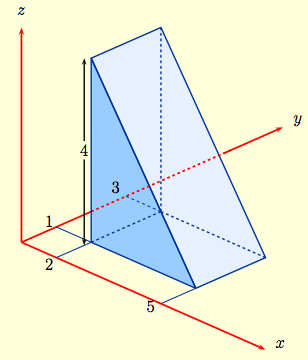
Example: Compute the integral $\iint_R \frac{4}{3}(5-x) dA$, where $R$ is the rectangle $[2,\,5]\,\times\,[1,\, 3]$ in the $xy$-plane. Solution: The integral is equal to the volume of the solid $W$ shown to the right, namely the region between the $x$-$y$ plane and the plane $z=\frac{4}{3}(5-x)$ and above $R$. To find its volume, take a vertical slice for fixed $y, \, 1 \le y \le 3$. The trace of the solid on the vertical plane is the same triangle for each $y$. But the triangle has height $=4$ and base $=3$, so it has area $$\frac{1}{2}\times \hbox{base}\times \hbox{height} \ = \ 6\,.$$ Thus $W$ has $$\hbox{volume} = \hbox{area triangle}\times \hbox{side-length} = 12, \qquad \hbox{and}$$ $$\iint_R \frac{4}{3}(5-x) dA = \hbox{ volume of $W$ } = 12.$$