Order of integration

Some regions can be viewed either as Type I or Type II. In that case we can set up an iterated integral in two ways. Depending on the integrand, one can be a lot easier than the other!

Sometimes you're given an impossible-looking iterated integral, and you can solve it by swapping (aka reversing) the order of integration. This means

1. Realizing that the iterated integral is a double integral over some region $D$.
2. Expressing $D$ as the other type of region (Type II if it was originally set up as Type I, and Type I if it was originally set up as Type II).
3. Re-writing the integral over $D$ as an interated integral in a new way. If had originally been $dx \,dy$, it should now be $dy \,dx$, and vice-versa.
4. Doing the new iterated integral.

An example is worked in detail in the video.

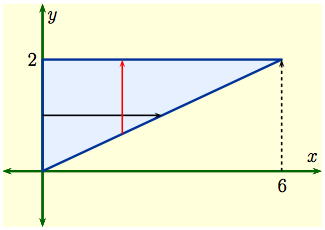
Example 1: Evaluate the integral $$I \ = \ \int \int_D\, x\,\sqrt{1+y^3}\, dA$$ when $D$ is the triangular region shown to the right enclosed by the $y$-axis and the lines $$y \ = \ \frac{1}{3}x\,, \qquad y \ = \ 2\,.$$

Bad Choice: Fix $x$ and integrate with respect $y$ along the red line. Then $$I \ = \ \int_0^6 \left(\int_{x/3}^2\, x\,\sqrt{1+y^3}\, dy\right)dx\,.$$ The trouble is that the inner integral involves requires

evaluating the integral $$\int_{x/3}^2\, \sqrt{1+y^3}\, dy\,.$$ Nothing you've learned so far in calculus will work here! The other order of integration is needed.

Good Choice: Fix $y$ and integrate with respect to $x$ along the black line. Then $$I \ = \ \int_0^2 \left(\int_{0}^{3y}\, x\,\sqrt{1+y^3}\, dy\right)dx\,.$$ Now the inner integral involves requires evaluating the integral

$$\int_{0}^{3y}\, x\, dx\ = \ \Bigl[\,\frac{1}{2}x^2\, \Bigr]_0^{3y} \ = \ \frac{9}{2}y^2\,.$$ In this case, $$I \ = \ \frac{9}{2} \int_0^2\, y^2 \, \sqrt{1+y^3}\,dy\ = \ 3\int_1^3\, u^2\, du\ = \ 26\,,$$ using the substitution $u^2 = 1+y^3$.

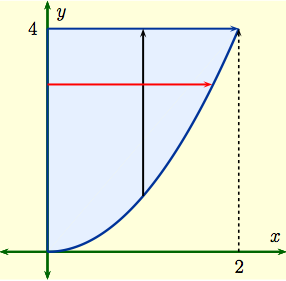
Example 2: Reverse the order of integration in the iterated integral $$I \ = \ \int _0^2\left(\int_{x^2}^4\, f(x,\,y)\, dy\right)dx\,,$$ but make no attempt to evaluate either integral.     Solution: The region of integration is the set $$D \ = \ \Bigl\{\,(x,\,y) : \, x^2 \le y \le 4\,, \ \ 0 \le x \le 2\,\Bigr\}$$ whose graph is shown to the right . The given repeated integral fixes $x$ and integrates with respect to $y$ along the vertical black line. To reverse the order of integration we need to fix $y$ and integrate with respect to $x$ along the red line. To set up the repeated integral we have to express $D$ in the form $$D \ = \ \Bigl\{\,(x,\,y) : \, \phi(y) \le x \le \psi(y)\,, \ \ c \le y \le d\,\Bigr\}$$ for suitably chosen $c,\, d$ and functions $\phi(y),\, \psi(y)$.     Now by inverse functions, the parabola $y = x^2$ can be written as $x = \sqrt{y}$; this tells us how to find the right hand limit of integration $x = \psi(y)$.

On the other hand, the graph above shows the left hand limit is $x = 0$. Thus $D$ can also be written as $$D \ = \ \Bigl\{\,(x,\,y) : \, 0 \le x \le \sqrt{y}\,, \ \ 0 \le y \le 4\,\Bigr\}\,.$$ Consequently, reversing the order of integration shows that $$I \ = \ \int _0^4\left(\int_0^{\sqrt{y}}\, f(x,\,y)\, dx\right)dy\,,$$ integrating now first with respect to $x$.

Warning: The tricky part of swapping the order of integration is re-writing the limits of integration. This involves studying the region of integration. $$\int_a^b \int_{y=g(x)}^{h(x)} f(x,y) dy\, dx$$ does NOT become $$\int_{g(x)}^{h(x)} \int_a^b f(x,y) dx\, dy \hbox{ !!}$$