Areas in the plane

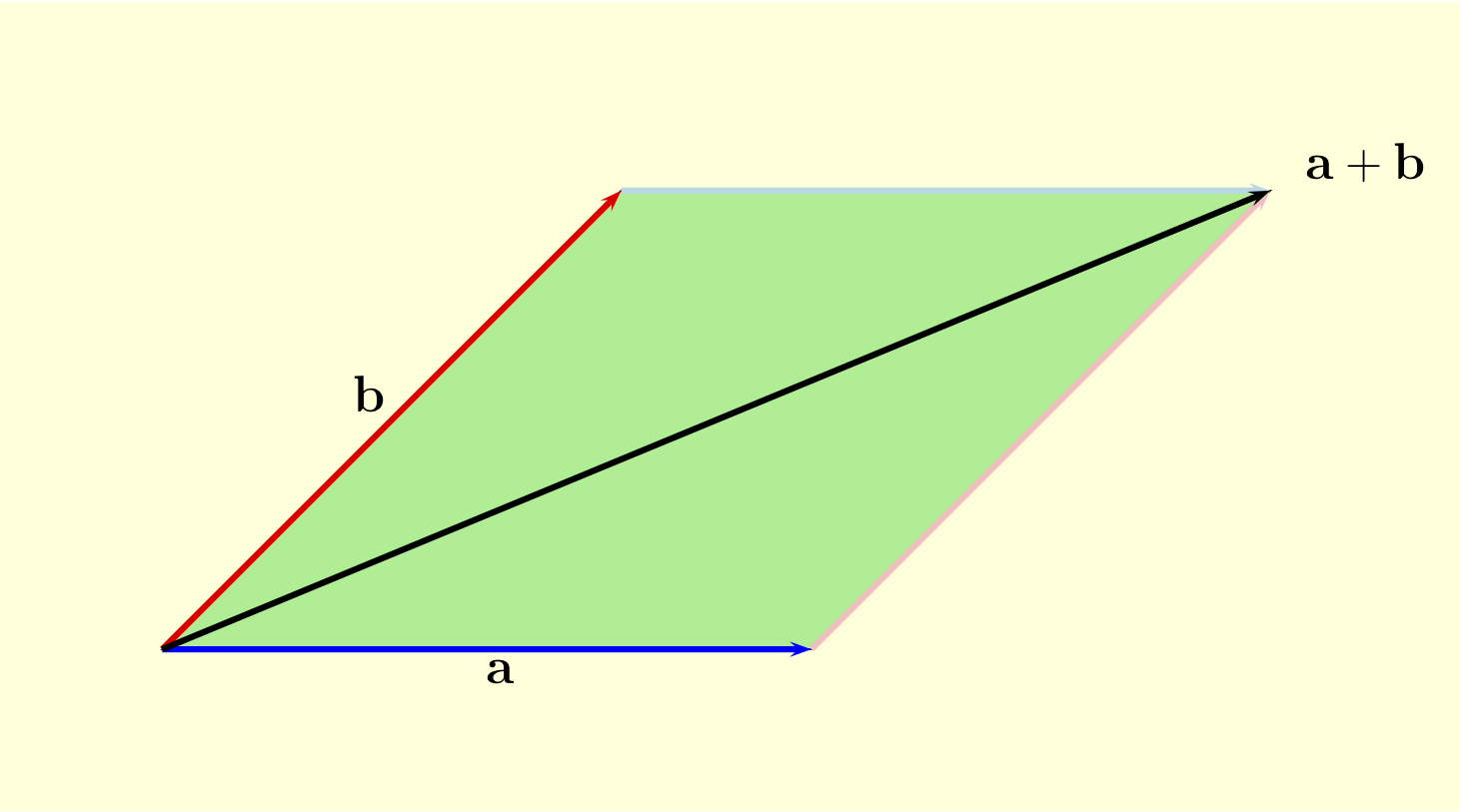
Areas in the plane: The idea behind cross products is a generalization of the formula for the area of a parallelogram in the plane. So suppose we have two vectors ${\bf a}= \langle a_1, a_2\rangle = a_1 {\bf i} + a_2 {\bf j}$ and ${\bf b}= \langle b_1, b_2\rangle = b_1 {\bf i} + b_2 {\bf j}$ in the plane. We want to compute the area $A({\bf a}, {\bf b})$ of the parallelogram with vertices at the origin, ${\bf a}$, ${\bf b}$ and ${\bf a}+{\bf b}$. This area function should have a few simple properties:

1. It should scale correctly: For any constant $\lambda$, $A(\lambda {\bf a},{\bf b})=A({\bf a}, \lambda {\bf b}) = \lambda A({\bf a},{\bf b})$. This forces us to allow $A({\bf a}, {\bf b})$ to be negative sometimes. If ${\bf b}$ is counter-clockwise of ${\bf a}$, then $A({\bf a}, {\bf b})$ is positive. If ${\bf b}$ is clockwise of ${\bf a}$, then $A({\bf a}, {\bf b})$ is minus the area of the parallelogram.
2. For any vectors ${\bf a}$, ${\bf b}$ and ${\bf c}$, $A({\bf a} + {\bf c}, {\bf b}) = A({\bf a}, {\bf b}) + A({\bf c}, {\bf b})$ and $A({\bf a}, {\bf b}+{\bf c}) = A({\bf a}, {\bf b}) + A({\bf a}, {\bf c})$ . The fancy mathematical term for properties (1) and (2) is that $A({\bf a},{\bf b})$ is a bilinear function of ${\bf a}$ and ${\bf b}$.
3. For any vector ${\bf a}$, $A({\bf a},{\bf a})=0$, since the "parallelogram" is squashed flat.

Notice that \begin{eqnarray*} 0 &=& A({\bf a}+{\bf b},{\bf a}+{\bf b}), \cr\cr &=& A({\bf a},{\bf a}) + A({\bf a},{\bf b}) + A({\bf b},{\bf a}) + A({\bf b},{\bf b}), \cr\cr &=& A({\bf a}, {\bf b}) + A({\bf b}, {\bf a}), \qquad \hbox{so} \cr \cr A({\bf b}, {\bf a}) &=& - A({\bf a}, {\bf b}).\end{eqnarray*} Unlike ordinary multiplication, the area function cares about which entry comes first. This means that $A({\bf i}, {\bf i})= A({\bf j}, {\bf j})= 0 $, that $A({\bf i}, {\bf j})=1$ (since ${\bf i}$ and ${\bf j}$ span the unit square), and that $A({\bf j}, {\bf i})=-1$.

Putting this together, we get the formula for area: \begin{eqnarray*}A({\bf a}, {\bf b}) & = & A(a_1 {\bf i}+ a_2{\bf j}, b_1 {\bf i}+ b_2{\bf j}) \cr \cr & = & a_1b_1 A({\bf i}, {\bf i}) + a_1b_2 A({\bf i}, {\bf j}) + a_2b_1 A({\bf j}, {\bf i}) + a_2b_2 A({\bf j}, {\bf j}) \cr \cr & = & a_1 b_2 - a_2 b_1. \end{eqnarray*} You may have seen this formula before as the determinant of the $2 \times 2$ matrix $$\left [\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array}\right ]\,.$$

The following video describes determinants of $2\times 2$ and $3 \times 3$ matrices, and explains how they are related to areas and volumes.