Definition of cross product

Cross Products p2 Cross Product: We now want 'multiplication' of vectors to produce a vector, ${\bf u}\times {\bf v}$, and not a scalar. Such a vector product occurs many times in geometry as well as in engineering and physics. To do that, we need matrices and determinants.

A $2 \times 2$ matrix is an array $$\left [\begin{array}{cc} a & b \\ c & d \end{array}\right ]\,,$$ where the entries $a,\, b, \,c$, and $d$ are scalars. Similarly, a $3 \times 3$ matrix is an array $$\left [\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right ]\,,$$ where the entries have been conveniently indexed to indicate the row and column they belong to. The determinant of a $2 \times 2$ matrix is given by $$\left |\begin{array}{cc} a & b \\ c & d \end{array}\right | \ =\ ad\,-\,bc\,,$$ while the determinant of a $3 \times 3$ matrix is $$\left|\begin{array}{ccc} X & Y & Z \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{array}\right| \ = \ X \left|\begin{array}{cc} a_2 & a_3 \\ b_2 & b_3 \end{array}\right| - Y \left|\begin{array}{cc} a_1 & a_3 \\ b_1 & b_3 \end{array}\right| + Z \left|\begin{array}{cc} a_1 & a_2 \\ b_1 & b_2 \end{array}\right| \qquad\qquad $$ $$\qquad \qquad = \ X(a_2b_3 - b_2a_3) - Y(a_1b_3 - b_1a_3) + Z(a_1b_2 - b_1a_2)\,,$$ the entries being labeled simply to emphasize how they get combined and multiplied.

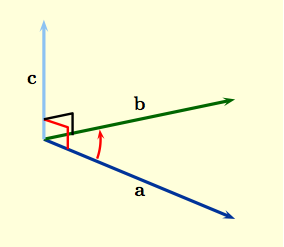
Because a vector has direction, a convention has to be adopted when defining the 'vector' product of two vectors. If ${\bf a}$, ${\bf b}$ are vectors arranged so that they have the same tail, then vectors $\{{\bf a},\, {\bf b},\, {\bf c}\}$ are said to form a right-handed system when ${\bf c}$ is perpendicular to the plane containing ${\bf a}$, ${\bf b}$ and points in the direction shown to the right.
Since there could be two directions for ${\bf c}$ to point and still be perpendicular to the plane containing ${\bf a}$ and ${\bf b}$, the right hand rule specifies which direction we'll choose. If you point your right hand along ${\bf a}$ and curl your fingers so they point along ${\bf b}$ then your extended thumb should be pointing along ${\bf c}$. Notice that $\{{\bf i},\, {\bf j},\, {\bf k}\}$ is a right-handed system.

Question: For a right-handed system $\{{\bf a},\, {\bf b},\, {\bf c}\}$,
   (i) Is $\{{\bf b},\, {\bf a},\, {\bf c}\}$ a right-handed system?
   (ii) Is $\{{\bf b},\, {\bf a},\, -{\bf c}\}$ a right-handed system? Answers: Switching ${\bf a},\,{\bf b}$ reverses the direction of ${\bf c}$, so
   (i) NO, $\ \{{\bf b},\, {\bf a},\, {\bf c}\}$ is not right-handed
   (ii) YES, $\ \{{\bf b},\, {\bf a},\, -{\bf c}\}$ is right-handed. $\quad $

Definition: The Cross Product, ${\bf u} \times {\bf v}$, of vectors $\bf u$ and $\bf v$ is the vector defined by $${\bf u} \times {\bf v}\ = \ (\|{\bf u}\|\|{\bf v}\| \sin \theta){\bf n}$$ where $ \theta $ is the angle between $\bf u$ and $\bf v$, and ${\bf n}$ is the unit vector perpendicular to ${\bf u}$ and ${\bf v}$ such that $\{{\bf u},\, {\bf v},\, {\bf n}\}$ forms a right-handed system. Since $\sin 0\,=\, \sin \pi \,=\, 0$, vectors ${\bf u}, \, {\bf v}$ are parallel when ${\bf u}\times {\bf v} \ = \ 0$ and ${\bf u},\, {\bf v} \, \ne\,0$.

Note that the cross product of two vectors is a vector. The magnitude of ${\bf u} \times {\bf v}$ is $\|{\bf u}\| \|{\bf v}\| \sin(\theta)$, and the direction of ${\bf u} \times {\bf v}$ is ${\bf n}$.

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Definition of cross product