M408M Learning Module Pages
Main page

Chapter 10: Parametric Equations and Polar Coordinates

Chapter 12: Vectors and the Geometry of Space

Learning module LM 12.1: 3-dimensional rectangular coordinates:

Learning module LM 12.2: Vectors:

Learning module LM 12.3: Dot products:

Learning module LM 12.4: Cross products:

       Areas in the plane
      Definition
      Computing cross products
      Applications

Learning module LM 12.5: Equations of Lines and Planes:

Learning module LM 12.6: Surfaces:

Chapter 13: Vector Functions

Chapter 14: Partial Derivatives

Chapter 15: Multiple Integrals

Applications

Cross Products p4

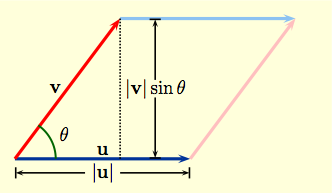
  Geometric Application 1: when vectors ${\bf u}$, ${\bf v}$ are adjacent sides of the parallelogram shown to right, then the height of the parallelogram is $\|{\bf v}\|\sin \theta$, so its $$\hbox{area} \ = \ \hbox{base $\times$ height} = \|{\bf u}\|\|{\bf v}\| \sin\theta = \|{\bf u} \times {\bf v}\|\,.$$ Thus the length of $\bf u \times \bf v$ is the area of the parallelogram whose sides are ${\bf u}$ and ${\bf v}$.

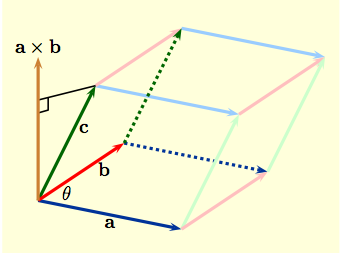
This should come as no surprise. If we have two vectors in the $x$-$y$ plane, ${\bf a} = a_1 {\bf i} + a_2 {\bf j}$ and ${\bf b} = b_1 {\bf i} + b_2 {\bf j}$, then ${\bf a} \times {\bf b} = (a_1b_2-a_2b_1){\bf k}$, and we already know that $a_1b_2-a_2b_1$ is the area of a parallelogram in the plane.

  Geometric Application 2: the vectors ${\bf a}$, ${\bf b}$ and ${\bf c}$ shown respectively in blue, red and green to the right form adjacent edges of a parallelepiped. Now by 1., the base has area $= \|{\bf a} \times {\bf b}\|$, while its $$\hbox{height} \ = \ \hbox{comp}_{{\bf a} \times {\bf b} }({\bf c}) \ = \ \frac{\|{\bf c}\,\cdot\,({\bf a} \times {\bf b} )\|}{\|{\bf a} \times {\bf b} \|}\,.$$ Thus the parallelepiped has $$ \hbox{volume}\ = \ \hbox{(area of base) $\times$ height} \ = \ \|{\bf c} \,\cdot \, ({\bf a} \times {\bf b}\ )\|\,.$$

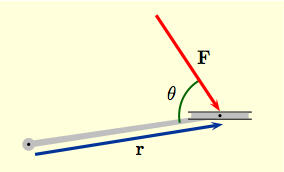
Remember that ${\bf c} \cdot ({\bf a} \times {\bf b})$ is the determinant of a $3 \times 3$ matrix whose rows are ${\bf c}$, ${\bf a}$ and ${\bf b}$. $3 \times 3$ determinants give volume the same way that $2 \times 2$ determinants give area.

  Mechanics Application 1: when we push down on a bike pedal we exert a force, a vector, on the bike pedal. The objective is to turn the chain wheel. In the figure to the right only the component $\|\sin \theta \, {\bf F}\|$ of ${\bf F}$ will have any effect. Torque as defined by the cross product $${\bf \tau}\ = \ {\bf r} \times {\bf F}\,,$$ is a measure of the turning force exerted as the cyclist pushes on the pedal. Note that the torque is perpendicular to the plane of rotation. In most examples, the direction of the torque is along the axis of rotation.


  Example: compute the volume of the parallelepiped with adjacent edges $\overline{OP}, \, \overline{OQ}$ and $\overline{OR}$ determined by vertices $$P(1,\,-1,\,-2),\ \ Q(1,\,1,\,-1),\ \ R(1,\,3,\,4),$$ where $O$ is the origin.

Solution: the parallelepiped is determined by $${\bf a} \ = \ \overrightarrow{OP}\ = \ \langle 1,\, -1,\, -2\rangle,$$ $${\bf b} \ = \ \overrightarrow{OP}\ = \ \langle 1,\, 1,\, -1\rangle,$$ $${\bf c} \ = \ \overrightarrow{OP}\ = \ \langle 1,\, 3,\, 4\rangle.$$ 		So its volume is given by scalar triple product $${\bf a} \,\cdot\, ({\bf b} \times {\bf c} ) \ = \ \left|\begin{array}{ccc} 1 & -1 & -2 \\ 1 & 1 & -1 \\ 1 & 3 & 4 \end{array}\right|\qquad \qquad$$ $$= \ \left|\begin{array}{cc} 1 & -1 \\ 3 & 4 \end{array}\right| - (-1)\left|\begin{array}{cc} 1 & -1 \\ 1 & 4 \end{array}\right| -2\left|\begin{array}{cc} 1 & 1 \\ 1 & 3 \end{array}\right| \,.$$ Consequently, the parallelepiped has $$ \hbox{volume}\ = \ 8\ \hbox{units}\,.$$


    Two very useful properties of the (scalar) triple product follow immediately from its interpretation as the volume of a parallelepiped: $${\bf u} \cdot ({\bf u} \times {\bf v}) \ = \ 0\,, \qquad {\bf v} \cdot ({\bf u} \times {\bf v}) \ = \ 0\,,$$ because in both cases the parallelepiped collapses to a parallelogram, and so has zero volume.