Astronomy

Home

Kepler's laws say that planets follow elliptical orbits around the sun, with the sun at a focus. In other words, the distance $r$ between a planet and the sun is given by $$r = \frac{ed}{1-e\cos(\theta-\theta_0)}.$$

Perihelion and Aphelion: The point $\theta=\theta_0+\pi$ where the planet is closest to the sun is called perihelion, and is at distance $\displaystyle{r = \frac{ed}{1+e}}$. The point $\theta=\theta_0$ where the planet is farthest from the sun is called aphelion, and is at distance $\displaystyle{r=\frac{ed}{1-e}}$. (The terms perihelion and aphelion come from the Greek word helios, meaning sun, and are only applied to orbits around the sun.)

Most planets have very low eccentricity, and their orbits are almost circles. The earth's eccentricity is only 0.0167, or 1.67%, so the distance to the sun at aphelion (around July 4) is about 3.3% farther than at perihelion (around January 3). As a result, the earth receives about 6.5% more sunlight in January than in July! [Note: seasons are caused by the tilt of the earth's axis, not by the eccentricity of the orbit.]

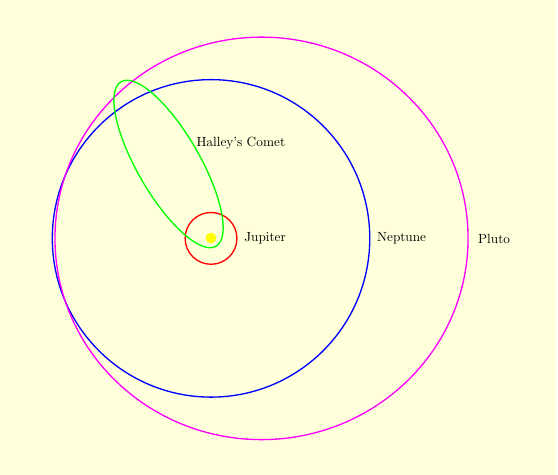
A few planets are a bit more eccentric. Mercury's eccentricity is about .2056. Pluto, no longer considered a planet, has an eccentricity of .248. At perihelion, Pluto is closer to the sun than Neptune. At aphelion, it is 60% farther.

Comets have very high eccentricity, close to 1. They start very far from the sun, plunge into the solar system, make a close pass, and then zip out again. Halley's Comet has an eccentricity of .967, meaning that at aphelion it is $\displaystyle{\frac{1+e}{1-e}\approx 60}$ times farther from the sun than at perihelion. Comet Hale-Bopp, the brightest comet ever seen when it passed the sun in 1997, had an eccentricity of .995. Its aphelion is about 400 times farther than its perihelion.

Occasionally, a comet will get a gravitational kick from a planet as it enters the solar system. This extra energy gives it an eccentricity slightly greater than 1. Comet C/1980 E1 had an eccentricity of 1.057. It followed a hyperbolic trajectory out of the solar system, and will never return.

Integration by Parts

Integrals of Trig Functions

Trig Substitutions

Partial Fractions

Strategies of Integration

Improper Integrals

Modeling with Differential Equations

Euler's Method and Direction Fields

Separable Equations

Models of Growth

Linear Equations

Parametrized Curves

Calculus with Parametrized Curves

Polar Coordinates

Areas and Lengths of Polar Curves

Conic sections

Conic Sections in Polar Coordinates

Infinite Sequences

Infinite Series

Integral Test

Comparison Tests

Convergence of Series with Negative Terms

The Ratio and Root Tests

Strategies for testing Series

Power Series

Representing Functions as Power Series

Taylor and Maclaurin Series

Applications of Taylor Polynomials

Functions of 2 and 3 variables

Partial Derivatives

Differentiability and the Chain Rule

Multiple Integrals

Iterated Integrals over Rectangles

Double Integrals over General Regions

Double integrals in polar coordinates

Multiple integrals in physics

Integrals in Probability and Statistics

Change of Variables