Integral Test

Home

Integration by Parts

Integration by Parts
Examples
Integration by Parts with a definite integral
Going in Circles
Tricks of the Trade

Integrals of Trig Functions

Antiderivatives of Basic Trigonometric Functions
Product of Sines and Cosines (mixed even and odd powers or only odd powers)
Product of Sines and Cosines (only even powers)
Product of Secants and Tangents
Other Cases

Trig Substitutions

How Trig Substitution Works
Summary of trig substitution options
Examples
Completing the Square

Partial Fractions

Introduction to Partial Fractions
Linear Factors
Irreducible Quadratic Factors
Improper Rational Functions and Long Division
Summary

Strategies of Integration

Substitution
Integration by Parts
Trig Integrals
Trig Substitutions
Partial Fractions

Improper Integrals

Type 1 - Improper Integrals with Infinite Intervals of Integration
Type 2 - Improper Integrals with Discontinuous Integrands
Comparison Tests for Convergence

Modeling with Differential Equations

Introduction
Separable Equations
A Second Order Problem

Euler's Method and Direction Fields

Euler's Method (follow your nose)
Direction Fields
Euler's method revisited

Separable Equations

The Simplest Differential Equations
Separable differential equations
Mixing and Dilution

Models of Growth

Exponential Growth and Decay
The Zombie Apocalypse (Logistic Growth)

Linear Equations

Linear ODEs: Working an Example
The Solution in General
Saving for Retirement

Parametrized Curves

Three kinds of functions, three kinds of curves
The Cycloid
Visualizing Parametrized Curves
Tracing Circles and Ellipses
Lissajous Figures

Calculus with Parametrized Curves

Video: Slope and Area
Video: Arclength and Surface Area
Summary and Simplifications
Higher Derivatives

Polar Coordinates

Definitions of Polar Coordinates
Graphing polar functions
Video: Computing Slopes of Tangent Lines

Areas and Lengths of Polar Curves

Area Inside a Polar Curve
Area Between Polar Curves
Arc Length of Polar Curves

Conic sections

Slicing a Cone
Ellipses
Hyperbolas
Parabolas and Directrices
Shifting the Center by Completing the Square

Conic Sections in Polar Coordinates

Foci and Directrices
Visualizing Eccentricity
Astronomy and Equations in Polar Coordinates

Infinite Sequences

Approximate Versus Exact Answers
Examples of Infinite Sequences
Limit Laws for Sequences
Theorems for and Examples of Computing Limits of Sequences
Monotonic Covergence

Infinite Series

Introduction
Geometric Series
Limit Laws for Series
Test for Divergence and Other Theorems
Telescoping Sums

Integral Test

Preview of Coming Attractions
The Integral Test
Estimates for the Value of the Series

Comparison Tests

The Basic Comparison Test
The Limit Comparison Test

Convergence of Series with Negative Terms

Introduction, Alternating Series,and the AS Test
Absolute Convergence
Rearrangements

The Ratio and Root Tests

The Ratio Test
The Root Test
Examples

Strategies for testing Series

Strategy to Test Series and a Review of Tests
Examples, Part 1
Examples, Part 2

Power Series

Radius and Interval of Convergence
Finding the Interval of Convergence
Power Series Centered at $x=a$

Representing Functions as Power Series

Functions as Power Series
Derivatives and Integrals of Power Series
Applications and Examples

Taylor and Maclaurin Series

The Formula for Taylor Series
Taylor Series for Common Functions
Adding, Multiplying, and Dividing Power Series
Miscellaneous Useful Facts

Applications of Taylor Polynomials

Taylor Polynomials
When Functions Are Equal to Their Taylor Series
When a Function Does Not Equal Its Taylor Series
Other Uses of Taylor Polynomials

Functions of 2 and 3 variables

Functions of several variables
Limits and continuity

Partial Derivatives

One variable at a time (yet again)
Definitions and Examples
An Example from DNA
Geometry of partial derivatives
Higher Derivatives
Differentials and Taylor Expansions

Differentiability and the Chain Rule

Differentiability
The First Case of the Chain Rule
Chain Rule, General Case
Video: Worked problems

Multiple Integrals

General Setup and Review of 1D Integrals
What is a Double Integral?
Volumes as Double Integrals

Iterated Integrals over Rectangles

How To Compute Iterated Integrals
Examples of Iterated Integrals
Fubini's Theorem
Summary and an Important Example

Double Integrals over General Regions

Type I and Type II regions
Examples 1-4
Examples 5-7
Swapping the Order of Integration
Area and Volume Revisited

Double integrals in polar coordinates

dA = r dr (d theta)
Examples

Multiple integrals in physics

Double integrals in physics
Triple integrals in physics

Integrals in Probability and Statistics

Single integrals in probability
Double integrals in probability

Change of Variables

Review: Change of variables in 1 dimension
Mappings in 2 dimensions
Jacobians
Examples
Bonus: Cylindrical and spherical coordinates

Estimates of Value of the Series

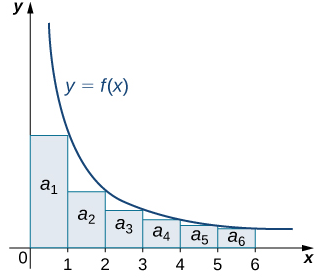
We include the previous graphics again, but this time to help us estimate the value of a series using concepts from the integral test. Remember that
$\displaystyle\sum_{n=1}^\infty a_n$ is equal to the sum of the areas of the rectangles $a_n$ from $n=1$ to infinity below,
$\displaystyle \int_1^\infty f(x)\, dx$ is the area under the curve $f$ from $x=1$ to infinity below, and that
$f(n)=a_n$.

Upper Estimate	$$ \sum_{n=1}^\infty a_n \le\, a_1 + \int_1^\infty f(x)\, dx$$ archive.cnx.org
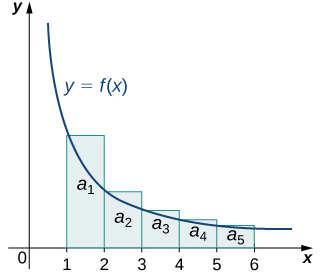
Lower Estimate	$$ \sum_{n=1}^\infty a_n \ge \int_1^\infty f(x) \,dx$$ archive.cnx.org
Bounds on series	$$ \int_1^\infty f(x) \,dx \le \sum_{n=1}^\infty a_n \le\, a_1 + \int_1^\infty f(x)\, dx$$	(after putting together the estimates from above)
Estimate of series	$$s_{n-1}+\int_n^\infty f(x)\,dx\le\sum_{i=1}^\infty a_i\le s_n+\int_n^\infty f(x)\,dx$$	Explained in the video.