Double Integrals over General Regions

Home

Examples 5-7

In the previous Examples 3 and 4, the way we specified $D$ and $R$ suggested how to write the integral as a iterated integral. Sometimes conditions are best interpreted graphically before deciding on whether to evaluate as Type I or Type II.

Example 5: Evaluate the integral $\displaystyle I \ = \iint_D\, (3x +4y)\, dA$,
where $D$ is the bounded region enclosed by $y = x$ and $y=x^2$.

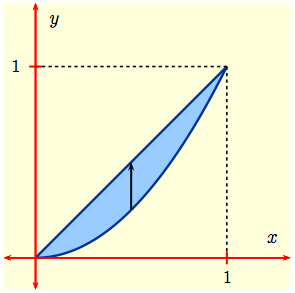
DO: Without looking, graph the region $D$. Set up a Type I integral.

Solution 5: $D$ is enclosed by the straight line $y = x$ and the parabola $y = x^2$ as shown here. To determine the limits of integration we first need to find the points of intersection of $y = x$ and $y = x^2$. These occur when $x^2 = x$. This means $x(x-1)=0$, so $x = 0,\, 1$.
Treating $D$ as a Type I region, we fix $x$ between $x=0$ and $x=1$, and integrate with respect to $y$ along the black vertical line, getting the iterated integral $\displaystyle I \ = \ \int_0^1\left(\int_{x^2}^{x}\, (3x + 4y)\, dy\right)\,dx$
DO: Evaluate $I$.

------------------------------------------------------------------------------

In Example 5 it was simpler to fix $x$ and integrate first with respect to $y$ because the bounding curves were already given to us in terms of $x$, as $$y \ = \ f_1(x)\ = \ x^2\,,\qquad y \ = \ f_2(x)\ = \ x\,.$$ Had they been given as $x \,=\, g_1(y)$ and $x\,=\, g_2(y)\,$ it might have been easier to think of $D$ as a Type II region. We would fix $y$ and first integrate with respect to $x$. Sometimes the geometry of the region of integration makes it obvious whether we have Type I or Type II, as in the following examples (which we will not evaluate).

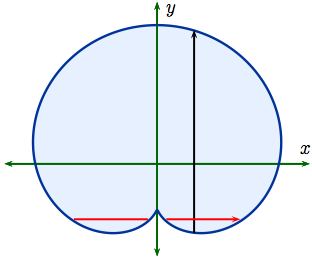
Example 6: The region $D$ that is shown here is Type I but is not Type II: Fixing $x$ and integrating first with respect to $y$ along the vertical black line makes good sense because then we have the same curve $f_1(x)$ along the bottom and $f_2(x)$ along the top: $$ D \ = \ \Bigl\{\,(x,\,y) : f_1(x) \le y \le f_2(x),\ \ a \le x \le b\,\Bigl\}$$ for suitable choices of $a,\, b$ and functions $f_1(x),\, f_2(x)$ giving us: $$ \iint_D\, f(x,\,y)\, dA = \int_a^b \left(\int_{f_1(x)}^{f_2(x)}\, f(x,\,y)\, dy\right) dx\,.$$But if we had chosen to fix $y$, then the integral with respect to $x$ would sometimes split into two parts, as is shown with the red horizontal lines. This would make evaluate of this integral more complicated -- for one thing, there would be more than one integral.

------------------------------------------------------------------------------

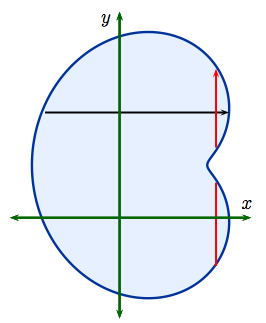
Example 7: Similarly, the region $D$ shown here is Type II but not Type I. Fixing $y$ and integrating first with respect to $x$ along the horizontal black line makes good sense because then $$ D \ = \ \Bigl\{\,(x,\,y) : g_1(y) \le x \le g_2(y),\ \ c \le y \le d\,\Bigl\}$$ for suitable choices of $c,\, d$ and functions $g_1(y),\, g_2(y)$. In this case $$ \iint_D\, f(x,\,y)\, dxdy = \int_c^d \left(\int_{g_1(y)}^{g_2(y)}\, f(x,\,y)\, dx\right) dy\,.$$But if we had chosen to fix $x$, then the integral with respect to $y$ would sometimes splits into two parts as shown by the red vertical lines. Again, this would make the integral(s) more complicated.

Integration by Parts

Integrals of Trig Functions

Trig Substitutions

Partial Fractions

Strategies of Integration

Improper Integrals

Modeling with Differential Equations

Euler's Method and Direction Fields

Separable Equations

Models of Growth

Linear Equations

Parametrized Curves

Calculus with Parametrized Curves

Polar Coordinates

Areas and Lengths of Polar Curves

Conic sections

Conic Sections in Polar Coordinates

Infinite Sequences

Infinite Series

Integral Test

Comparison Tests

Convergence of Series with Negative Terms

The Ratio and Root Tests

Strategies for testing Series

Power Series

Representing Functions as Power Series

Taylor and Maclaurin Series

Applications of Taylor Polynomials

Functions of 2 and 3 variables

Partial Derivatives

Differentiability and the Chain Rule

Multiple Integrals

Iterated Integrals over Rectangles

Double Integrals over General Regions

Double integrals in polar coordinates

Multiple integrals in physics

Integrals in Probability and Statistics

Change of Variables

Examples 5-7