Integral Test

Home

The Fundamental Theorem of Calculus

Three Different Concepts
The Fundamental Theorem of Calculus (Part 2)
The Fundamental Theorem of Calculus (Part 1)
More FTC 1

The Indefinite Integral and the Net Change

Indefinite Integrals and Anti-derivatives
A Table of Common Anti-derivatives
The Net Change Theorem
The NCT and Public Policy

Substitution

Substitution for Indefinite Integrals
Examples to Try
Revised Table of Integrals
Substitution for Definite Integrals
Examples

Area Between Curves

Computation Using Integration
To Compute a Bulk Quantity
The Area Between Two Curves
Horizontal Slicing
Summary

Volumes

Slicing and Dicing Solids
Solids of Revolution 1: Disks
Solids of Revolution 2: Washers
More Practice

Integration by Parts

Integration by Parts
Examples
Integration by Parts with a definite integral
Going in Circles
Tricks of the Trade

Integrals of Trig Functions

Antiderivatives of Basic Trigonometric Functions
Product of Sines and Cosines (mixed even and odd powers or only odd powers)
Product of Sines and Cosines (only even powers)
Product of Secants and Tangents
Other Cases

Trig Substitutions

How Trig Substitution Works
Summary of trig substitution options
Examples
Completing the Square

Partial Fractions

Introduction
Linear Factors
Irreducible Quadratic Factors
Improper Rational Functions and Long Division
Summary

Strategies of Integration

Substitution
Integration by Parts
Trig Integrals
Trig Substitutions
Partial Fractions

Improper Integrals

Type 1 - Improper Integrals with Infinite Intervals of Integration
Type 2 - Improper Integrals with Discontinuous Integrands
Comparison Tests for Convergence

Differential Equations

Introduction
Separable Equations
Mixing and Dilution

Models of Growth

Exponential Growth and Decay
Logistic Growth

Infinite Sequences

Approximate Versus Exact Answers
Examples of Infinite Sequences
Limit Laws for Sequences
Theorems for and Examples of Computing Limits of Sequences
Monotonic Covergence

Infinite Series

Introduction
Geometric Series
Limit Laws for Series
Test for Divergence and Other Theorems
Telescoping Sums and the FTC

Integral Test

Road Map
The Integral Test
Estimates of Value of the Series

Comparison Tests

The Basic Comparison Test
The Limit Comparison Test

Convergence of Series with Negative Terms

Introduction, Alternating Series,and the AS Test
Absolute Convergence
Rearrangements

The Ratio and Root Tests

The Ratio Test
The Root Test
Examples

Strategies for testing Series

Strategy to Test Series and a Review of Tests
Examples, Part 1
Examples, Part 2

Power Series

Radius and Interval of Convergence
Finding the Interval of Convergence
Power Series Centered at

$x=a$

Representing Functions as Power Series

Functions as Power Series
Derivatives and Integrals of Power Series
Applications and Examples

Taylor and Maclaurin Series

The Formula for Taylor Series
Taylor Series for Common Functions
Adding, Multiplying, and Dividing Power Series
Miscellaneous Useful Facts

Applications of Taylor Polynomials

Taylor Polynomials
When Functions Are Equal to Their Taylor Series
When a Function Does Not Equal Its Taylor Series
Other Uses of Taylor Polynomials

Partial Derivatives

Visualizing Functions in 3 Dimensions
Definitions and Examples
An Example from DNA
Geometry of Partial Derivatives
Higher Order Derivatives
Differentials and Taylor Expansions

Multiple Integrals

Background
What is a Double Integral?
Volumes as Double Integrals

Iterated Integrals over Rectangles

How To Compute Iterated Integrals
Examples of Iterated Integrals
Cavalieri's Principle
Fubini's Theorem
Summary and an Important Example

Double Integrals over General Regions

Type I and Type II regions
Examples 1-4
Examples 5-7
Order of Integration

The Integral Test

Integral Test: If

$f$ is a continuous, positive and decreasing function where

$f(n)=a_n$ on the interval

$[1,\infty)$ , then
the improper integral

$\displaystyle\int_1^\infty f(x)\, dx$ and the infinite series

$\displaystyle\sum_{n=1}^\infty a_n$
either both converge or both diverge.

Picture infinitely many rectangles of width 1 and height

$a_n$ , so the area of the

$n^{th}$ rectangle is

$a_n$ . Then the series

$\displaystyle\sum_{n=1}^\infty a_n$ is equal to the sum of the areas of these infinitely many rectangles. See the graphic examples below.

Consider this graph. We see that the value of the series from

$a_2$ on is less than the area under the curve

$f$ from 1 to infinity; i.e.

$\displaystyle\sum_{n=2}^\infty a_n<\int_1^\infty f(x)\,dx$ . If this integral converges to some finite value

$C$ , then by using this inequality and doing a little work, we get

$\displaystyle\sum_{n=1}^\infty a_n= a_1+\sum_{n=2}^\infty a_n<a_1+\int_1^\infty f(x)\,dx=a_1+C<\infty$ , so the series is finite, and thus the series converges.

archive.cnx.org

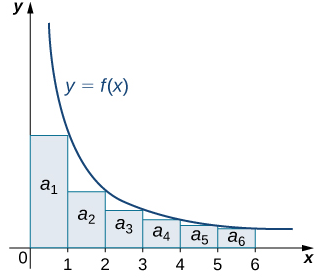Now consider this graph. We see that the sum of the same series beginning with

$a_1$ is larger than the area under the same curve

$f$ from 1 to infinity; i.e.

$\displaystyle\int_1^\infty f(x)\,dx<\sum_{n=1}^\infty a_n$ . If this integral diverges, then because of our constraints on

$f$ it diverges to infinity. Since the area under

$f$ is infinite, then the sum of the areas of the rectangles must also be infinite, i.e.

$\displaystyle\sum_{n=1}^\infty a_n$ is infinite, and thus the series diverges. We see that if the integral diverges, so does the series.

archive.cnx.org

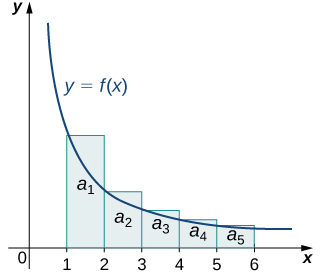Summary: either both the integral and the series converge, or both diverge.

From our work with improper integrals, you may have seen that the improper integral

$\displaystyle\int_1^\infty\frac{1}{x^p}\,dx$ converges if

$p>1$ , and diverges if

$p\le 1$ .

By using the integral test, we therefore get our $p$ -series test, which is extremely useful, especially when used to find comparable series for the comparison tests.

$\displaystyle{\sum_{n=1}^\infty \frac{1}{n^p}}$ converges if

$p>1$ and diverges if

$p \le 1$ .

Explanation and examples of the integral test, as well as determining the above integral of

$\frac{1}{x^p}$ and the

$p$ -series test are included on the first video. The second video includes detail of the graphical information above.