Home
The Fundamental Theorem of Calculus
Three Different ConceptsThe Fundamental Theorem of Calculus (Part 2)
The Fundamental Theorem of Calculus (Part 1)
More FTC 1
The Indefinite Integral and the Net Change
Indefinite Integrals and Anti-derivativesA Table of Common Anti-derivatives
The Net Change Theorem
The NCT and Public Policy
Substitution
Substitution for Indefinite IntegralsExamples to Try
Revised Table of Integrals
Substitution for Definite Integrals
Examples
Area Between Curves
Computation Using IntegrationTo Compute a Bulk Quantity
The Area Between Two Curves
Horizontal Slicing
Summary
Volumes
Slicing and Dicing SolidsSolids of Revolution 1: Disks
Solids of Revolution 2: Washers
More Practice
Integration by Parts
Integration by PartsExamples
Integration by Parts with a definite integral
Going in Circles
Tricks of the Trade
Integrals of Trig Functions
Antiderivatives of Basic Trigonometric FunctionsProduct of Sines and Cosines (mixed even and odd powers or only odd powers)
Product of Sines and Cosines (only even powers)
Product of Secants and Tangents
Other Cases
Trig Substitutions
How Trig Substitution WorksSummary of trig substitution options
Examples
Completing the Square
Partial Fractions
IntroductionLinear Factors
Irreducible Quadratic Factors
Improper Rational Functions and Long Division
Summary
Strategies of Integration
SubstitutionIntegration by Parts
Trig Integrals
Trig Substitutions
Partial Fractions
Improper Integrals
Type 1 - Improper Integrals with Infinite Intervals of IntegrationType 2 - Improper Integrals with Discontinuous Integrands
Comparison Tests for Convergence
Differential Equations
IntroductionSeparable Equations
Mixing and Dilution
Models of Growth
Exponential Growth and DecayLogistic Growth
Infinite Sequences
Approximate Versus Exact AnswersExamples of Infinite Sequences
Limit Laws for Sequences
Theorems for and Examples of Computing Limits of Sequences
Monotonic Covergence
Infinite Series
IntroductionGeometric Series
Limit Laws for Series
Test for Divergence and Other Theorems
Telescoping Sums and the FTC
Integral Test
Road MapThe Integral Test
Estimates of Value of the Series
Comparison Tests
The Basic Comparison TestThe Limit Comparison Test
Convergence of Series with Negative Terms
Introduction, Alternating Series,and the AS TestAbsolute Convergence
Rearrangements
The Ratio and Root Tests
The Ratio TestThe Root Test
Examples
Strategies for testing Series
Strategy to Test Series and a Review of TestsExamples, Part 1
Examples, Part 2
Power Series
Radius and Interval of ConvergenceFinding the Interval of Convergence
Power Series Centered at $x=a$
Representing Functions as Power Series
Functions as Power SeriesDerivatives and Integrals of Power Series
Applications and Examples
Taylor and Maclaurin Series
The Formula for Taylor SeriesTaylor Series for Common Functions
Adding, Multiplying, and Dividing Power Series
Miscellaneous Useful Facts
Applications of Taylor Polynomials
Taylor PolynomialsWhen Functions Are Equal to Their Taylor Series
When a Function Does Not Equal Its Taylor Series
Other Uses of Taylor Polynomials
Partial Derivatives
Visualizing Functions in 3 DimensionsDefinitions and Examples
An Example from DNA
Geometry of Partial Derivatives
Higher Order Derivatives
Differentials and Taylor Expansions
Multiple Integrals
BackgroundWhat is a Double Integral?
Volumes as Double Integrals
Iterated Integrals over Rectangles
How To Compute Iterated IntegralsExamples of Iterated Integrals
Cavalieri's Principle
Fubini's Theorem
Summary and an Important Example
Double Integrals over General Regions
Type I and Type II regionsExamples 1-4
Examples 5-7
Order of Integration
The Geometry of Partial Derivatives
|
Slopes in three dimensions
At a point $P(a,b,z)=(a,\,b,\, f(a,\,b))$ on the graph of
$z = f(x,\, y)$,
$\displaystyle\frac{\partial f}{\partial y}\Bigl|_{(a,\,b)}=f_y(a,b)$ represents the slope in the $y$-direction at $P$. |
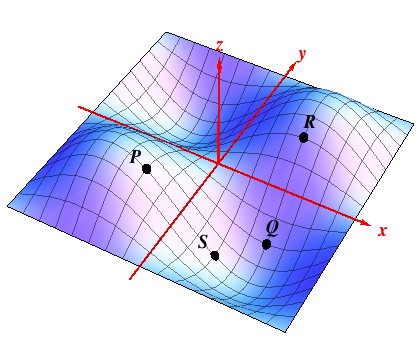
| Example 1:
Consider the surface $z=f(x,y)$ to the right, and determine
whether $f_x$ and $f_y$ are positive, negative, or zero at
the points $P,\ Q, \ R,$ and $S$ on the surface. (Be aware
of the placement of the axes.) Solution 1: at $Q$, for instance, the surface slopes up for fixed $x$ as $y$ increases, so $f_y\bigl|_{Q} > 0$, while the surface seems to remain at a constant height at $Q$ in the $x$ direction for fixed $y$, so $f_x\bigl|_{Q}= 0$. Considering the points $R$ and $P$, it appears that $$f_x\bigl|_{R} \,<\,0,\quad f_y\bigl|_{R} \,>\, 0\,, \qquad f_x\bigl|_{P} \,<\, 0,\, \quad f_y\bigl|_{P} \,=\, 0 \,.$$ DO: what happens at $S$? (answer at bottom of page) |
|
Information about the partial derivatives of a function $z = f(x,\,y)$ can be detected also from a contour map of $f$. Indeed, as one knows from using contour maps to learn whether a path on a mountain is going up or down, or how steep it is, so the sign of the partial derivatives of $z = f(x,y)$ and relative size can be read off from the contour map of $f$.
|
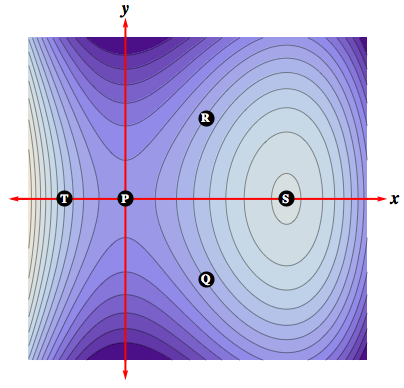
Example 2: To the right is the contour map of the function
$$z=f(x,y)= 3x^2 -y^2 -x^3 +2.$$ Here, the positive $z$
direction is coming toward you out of the page, with higher ground in lighter colors
and lower ground in darker colors.
Determine whether $f_x,\, f_y$ are positive, negative, or
zero at $P,\, Q,\, R,\, S$, and $T$. These are not the
same points as before! At $R$, for instance, are the contours increasing or decreasing as $y$ increases for fixed $x$? That will indicate the sign of $f_y$. But what happens at $P$ or at $S$? DO: Determine the sign of these partial derivatives. (answer at bottom of page) |
|
Solution 1 (continued): It appears that $\displaystyle f_x\bigl|_{S} \,<\,0,\quad f_y\bigl|_{S} \,=\, 0\,.$
-------------------------------------------------------------------------------
Solution 2: It appears that $\quad f_x\big|_R>0,\quad f_y\big|_R<0,\quad f_x\big|_S=0,\quad f_y\big|_S=0, \quad f_x\big|_Q>0,\quad f_y\big|_Q=0,\quad$ $ f_x\big|_P=f_y\big|_P=0,\quad f_x\big|_T<0,\quad f_y\big|_T=0$All the same ideas carry over in exactly the same way to functions $w = f(x,\,y,\,z)$ of three or more variables - just don't expect lots of pictures!! The partial derivative $f_z$, for instance, is simply the derivative of $f(x,\,y,\,z)$ with respect to $z$, keeping both of the variables $x$ and $y$ fixed.