
Home
The Fundamental Theorem of Calculus
Three Different QuantitiesThe Whole as Sum of Partial Changes
The Indefinite Integral as Antiderivative
The FTC and the Chain Rule
The Indefinite Integral and the Net Change
Indefinite Integrals and Anti-derivativesA Table of Common Anti-derivatives
The Net Change Theorem
The NCT and Public Policy
Substitution
Substitution for Indefinite IntegralsRevised Table of Integrals
Substitution for Definite Integrals
Area Between Curves
The Slice and Dice PrincipleTo Compute a Bulk Quantity
The Area Between Two Curves
Horizontal Slicing
Summary
Volumes
Slicing and Dicing SolidsSolids of Revolution 1: Disks
Solids of Revolution 2: Washers
Volumes Rotating About the $y$-axis
Integration by Parts
Behind IBPExamples
Going in Circles
Tricks of the Trade
Integrals of Trig Functions
Basic Trig FunctionsProduct of Sines and Cosines (1)
Product of Sines and Cosines (2)
Product of Secants and Tangents
Other Cases
Trig Substitutions
How it worksExamples
Completing the Square
Partial Fractions
IntroductionLinear Factors
Quadratic Factors
Improper Rational Functions and Long Division
Summary
Strategies of Integration
SubstitutionIntegration by Parts
Trig Integrals
Trig Substitutions
Partial Fractions
Improper Integrals
Type I IntegralsType II Integrals
Comparison Tests for Convergence
Differential Equations
IntroductionSeparable Equations
Mixing and Dilution
Models of Growth
Exponential Growth and DecayLogistic Growth
Infinite Sequences
Close is Good Enough (revisited)Examples
Limit Laws for Sequences
Monotonic Convergence
Infinite Series
IntroductionGeometric Series
Limit Laws for Series
Telescoping Sums and the FTC
Integral Test
Road MapThe Integral Test
When the Integral Diverges
When the Integral Converges
Comparison Tests
The Basic Comparison TestThe Limit Comparison Test
Convergence of Series with Negative Terms
IntroductionAlternating Series and the AS Test
Absolute Convergence
Rearrangements
The Ratio and Root Tests
The Ratio TestThe Root Test
Examples
Strategies for testing Series
List of Major Convergence TestsExamples
Power Series
Radius and Interval of ConvergenceFinding the Interval of Convergence
Other Power Series
Representing Functions as Power Series
Functions as Power SeriesDerivatives and Integrals of Power Series
Applications and Examples
Taylor and Maclaurin Series
The Formula for Taylor SeriesTaylor Series for Common Functions
Adding, Multiplying, and Dividing Power Series
Miscellaneous Useful Facts
Applications of Taylor Polynomials
What are Taylor Polynomials?How Accurate are Taylor Polynomials?
What can go Wrong?
Other Uses of Taylor Polynomials
Partial Derivatives
Definitions and RulesThe Geometry of Partial Derivatives
Higher Order Derivatives
Differentials and Taylor Expansions
Multiple Integrals
BackgroundWhat is a Double Integral?
Volumes as Double Integrals
Iterated Integrals over Rectangles
One Variable at the TimeFubini's Theorem
Notation and Order
Double Integrals over General Regions
Type I and Type II regionsExamples
Order of Integration
Area and Volume Revisited
Geometric Series
A geometric series is a series where the ratio between successive terms is constant. For example, the series $$ \sum_{i=0}^\infty\left(\frac{1}{3}\right)^i=1+\frac13+\frac19+\frac{1}{27}+\ldots $$ is geometric with ratio $r=\frac13$.
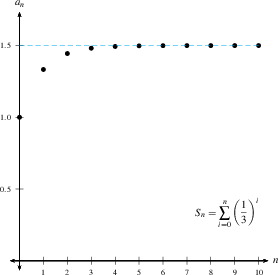
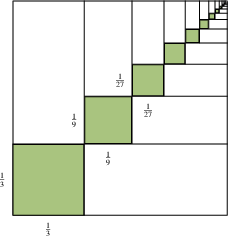
| The geometric series $\displaystyle\sum_{i=0}^\infty r^i=1+r+r^2+r^3 + \ldots$ converges to $\displaystyle\frac{1}{1-r}$ if $\lvert r\rvert <1$ and diverges if $\lvert r\rvert\ge1$. |