Home

The Fundamental Theorem of Calculus

Three Different Quantities
The Whole as Sum of Partial Changes
The Indefinite Integral as Antiderivative
The FTC and the Chain Rule

The Indefinite Integral and the Net Change

Indefinite Integrals and Anti-derivatives
A Table of Common Anti-derivatives
The Net Change Theorem
The NCT and Public Policy

Substitution

Substitution for Indefinite Integrals
Revised Table of Integrals
Substitution for Definite Integrals

Area Between Curves

The Slice and Dice Principle
To Compute a Bulk Quantity
The Area Between Two Curves
Horizontal Slicing
Summary

Volumes

Slicing and Dicing Solids
Solids of Revolution 1: Disks
Solids of Revolution 2: Washers
Volumes Rotating About the $y$-axis

Integration by Parts

Behind IBP
Examples
Going in Circles
Tricks of the Trade

Integrals of Trig Functions

Basic Trig Functions
Product of Sines and Cosines (1)
Product of Sines and Cosines (2)
Product of Secants and Tangents
Other Cases

Trig Substitutions

How it works
Examples
Completing the Square

Partial Fractions

Introduction
Linear Factors
Quadratic Factors
Improper Rational Functions and Long Division
Summary

Strategies of Integration

Substitution
Integration by Parts
Trig Integrals
Trig Substitutions
Partial Fractions

Improper Integrals

Type I Integrals
Type II Integrals
Comparison Tests for Convergence

Differential Equations

Introduction
Separable Equations
Mixing and Dilution

Models of Growth

Exponential Growth and Decay
Logistic Growth

Infinite Sequences

Close is Good Enough (revisited)
Examples
Limit Laws for Sequences
Monotonic Convergence

Infinite Series

Introduction
Geometric Series
Limit Laws for Series
Telescoping Sums and the FTC

Integral Test

Road Map
The Integral Test
When the Integral Diverges
When the Integral Converges

Comparison Tests

The Basic Comparison Test
The Limit Comparison Test

Convergence of Series with Negative Terms

Introduction
Alternating Series and the AS Test
Absolute Convergence
Rearrangements

The Ratio and Root Tests

The Ratio Test
The Root Test
Examples

Strategies for testing Series

List of Major Convergence Tests
Examples

Power Series

Radius and Interval of Convergence
Finding the Interval of Convergence
Other Power Series

Representing Functions as Power Series

Functions as Power Series
Derivatives and Integrals of Power Series
Applications and Examples

Taylor and Maclaurin Series

The Formula for Taylor Series
Taylor Series for Common Functions
Adding, Multiplying, and Dividing Power Series
Miscellaneous Useful Facts

Applications of Taylor Polynomials

What are Taylor Polynomials?
How Accurate are Taylor Polynomials?
What can go Wrong?
Other Uses of Taylor Polynomials

Partial Derivatives

Definitions and Rules
The Geometry of Partial Derivatives
Higher Order Derivatives
Differentials and Taylor Expansions

Multiple Integrals

Background
What is a Double Integral?
Volumes as Double Integrals

Iterated Integrals over Rectangles

One Variable at the Time
Fubini's Theorem
Notation and Order

Double Integrals over General Regions

Type I and Type II regions
Examples
Order of Integration
Area and Volume Revisited


How it works

Regular $u$-substitution works by setting $u=g(x)$ for some function $g$. We have to pick $u$ so that the integrand becomes a nice function of $u$ times $du$. In the video, we explore inverse substitutions.

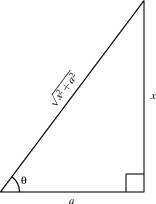
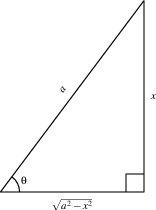
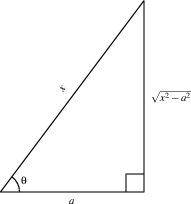
With inverse substitutions, we let $x = g(\theta)$, where typically $g$ is a trig function. Then $dx = g'(\theta)\, d\theta$, and we can always rewrite the integrand in terms of $\theta$ and $d\theta$. The tricky part is converting everything back to $x$ at the end of the problem.

There are three very useful trig substitution:

  1. For integrals involving $x^2 + a^2$ or $\sqrt{x^2+a^2}$, use $x = a \tan(\theta)$.

    Then $dx = a\, \sec^2(\theta)\, d\theta$ and $x^2+a^2 = a^2 \sec^2(\theta)$. To convert back to $x$, draw a right triangle with opposite side $x$, adjacent side $a$ and hypotenuse $\sqrt{x^2+a^2}$ and use soh-cah-toa.

  2. For integrals involving $a^2 - x^2$ or $\sqrt{a^2-x^2}$, use $x=a \sin(\theta)$.

    Then $dx = a \cos(\theta) d\theta$ and $\sqrt{a^2-x^2}= a \cos(\theta)$. To convert back to $x$, draw a right triangle with opposite side $x$, hypotenuse $a$ and adjacent side $\sqrt{a^2-x^2}$ and use soh-cah-toa.

  3. For integrals involving $x^2-a^2 $ or $\sqrt{x^2-a^2}$, use $x=a \sec(\theta)$.

    Then $dx = a \sec(\theta) \tan(\theta)\, d\theta$ and $\sqrt{x^2-a^2}= a \tan(\theta)$. To convert back to $x$, draw a right triangle with adjacent side $a$, hypotenuse $x$ and opposite side $\sqrt{x^2-a^2}$ and use soh-cah-toa.