Multiple Integrals

Home

Volumes as Double Integrals

Double integrals can be viewed as volumes in the same way that we view regular integrals as areas. This cuts two ways. We can compute volumes by doing double integrals. We can also understand double integrals by using what we already know about 3-dimensional geometry!

For $z=f(x,\,y) \ge 0$ and $R$ is a rectangle in the $xy$-plane, then the Double Integral $$ \int\int_R\, f(x,\,y)\, dx \,dy $$ of $f$ over $R$ equals the volume of the solid under the graph of $f$ and above $R$.

Example: Compute the integral $\iint_R \frac{4}{3}(5-x) \,dA$, where $R$ is the rectangle $[2,\,5]\,\times\,[1,\, 3]$ in the $xy$-plane.

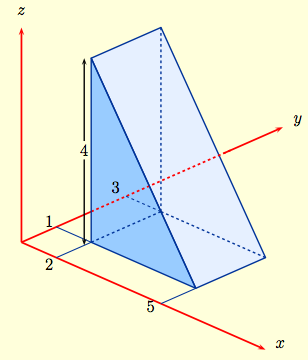
Solution: The integral is equal to the volume of the solid $W$ shown to the right, namely the region between the $x$-$y$ plane and the plane $z=\frac{4}{3}(5-x)$ and above $R$. To find its volume, take a vertical slice for fixed $y, \, 1 \le y \le 3$. The trace of the solid on the vertical plane is the same triangle for each $y$. But the triangle has height $=4$ and base $=3$, so it has area $$\frac{1}{2}\times \hbox{base}\times \hbox{height} \ = \ 6\,.$$ Thus $W$ has $$\hbox{volume} = \hbox{area triangle}\times \hbox{side-length} = 12, $$ and $$\iint_R \frac{4}{3}(5-x)\, dA = \hbox{ volume of $W$ } = 12.$$

The Fundamental Theorem of Calculus

The Indefinite Integral and the Net Change

Substitution

Area Between Curves

Volumes

Integration by Parts

Integrals of Trig Functions

Trig Substitutions

Partial Fractions

Strategies of Integration

Improper Integrals

Differential Equations

Models of Growth

Infinite Sequences

Infinite Series

Integral Test

Comparison Tests

Convergence of Series with Negative Terms

The Ratio and Root Tests

Strategies for testing Series

Power Series

Representing Functions as Power Series

Taylor and Maclaurin Series

Applications of Taylor Polynomials

Partial Derivatives

Multiple Integrals

Iterated Integrals over Rectangles

Double Integrals over General Regions

Volumes as Double Integrals